Casimireffect
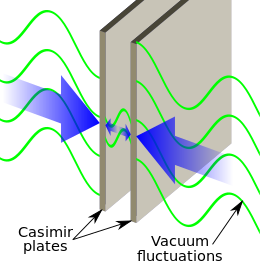
Het casimireffect is het natuurkundige verschijnsel waarbij twee elektrisch neutraal geladen metalen platen in een vacuüm door kwantumfluctuaties (zeer geringe) krachten ondervinden die ze naar elkaar toe drijven. Hendrik Casimir en Dirk Polder voorspelden dit verschijnsel in 1948.[1] Andere namen voor dit verschijnsel zijn Casimir-Polderkracht en Casimirkracht.
Verklaring[bewerken | brontekst bewerken]
Omdat deze aantrekkende kracht sterk afneemt met de afstand (namelijk met de vierde macht) is het effect alleen meetbaar bij uiterst kleine tussenafstanden. De kracht wordt veroorzaakt doordat alleen virtuele deeltjes met een bepaalde golflengte tussen de twee platen passen. Andere golflengtes worden uitgedempt. Hierdoor is het aantal deeltjes tussen de platen kleiner dan het aantal daarbuiten en worden de platen naar elkaar geduwd. Het effect kan ook gezien worden als een resonantie van de vacuümenergie tussen de platen. Op korte afstand is de Casimirkracht voor ongeladen platen de overheersende kracht.
Meting[bewerken | brontekst bewerken]
Hans Sparnaay van Philips in Eindhoven deed in 1958 een van de eerste metingen met een moeilijk experiment.[2] De resultaten waren niet in strijd met de theorie maar kampten met grote meetfouten. Steve K. Lamoreaux van het Los Alamos National Laboratory en Umar Mohideen en Anushree Roy van de University of California te Riverside deden in 1997 een nauwkeuriger meting. Via een uiterst nauwkeurige torsieslinger slaagde Lamoreaux erin om in vacuüm de casimirkracht te meten tussen een verguld bolletje van 4 cm in diameter en een verguld kwartsplaatje.[3] Mohideen en Roy toetsten het effect experimenteel met een hefboompje van een atoomkrachtmicroscoop met daarop een verguld bolletje van 200 μm.[4] Daarmee werd dit kwantumeffect proefondervindelijk aangetoond binnen 15% van de voorspelde waarde van de kracht. In 2001 slaagde een onderzoeksgroep van de Universiteit van Padua erin de casimirkracht tussen parallelle platen te meten met behulp van microresonatoren.
Formule[bewerken | brontekst bewerken]
Een uitdrukking voor deze casimirkracht kan met heuristische argumenten (op een voorfactor na) gevonden worden.
De kracht is evenredig met de oppervlakte A van de platen. Dat de platen van metaal moeten zijn om het effect waar te nemen duidt erop dat het om een elektromagnetisch verschijnsel gaat. De virtuele deeltjes zijn virtuele fotonen. Daarom komt de elektromagnetische constante bij uitstek, de lichtsnelheid c, in de formule voor. Omdat het een kwantummechanisch effect is, is ook constante van Planck h nodig. Een eenhedenanalyse laat zien dat de kracht omgekeerd evenredig moet zijn met de vierde macht van de afstand a tussen de platen. Een formele afleiding geeft hetzelfde resultaat en tevens de voorfactor (die negatief is aangezien het een aantrekkende kracht betreft). De formule voor de kracht luidt
Toepassing en omkering[bewerken | brontekst bewerken]
Professor Ulf Leonhardt en Dr. Thomas Philbin van de Universiteit van St Andrews in Schotland, hebben een manier gevonden om het verschijnsel om te keren, zodat het afstoot in plaats van aantrekt.[5]
Bronnen, noten en/of referenties
|

