Formule van Brahmagupta

Vierhoek in een ingeschreven cirkel

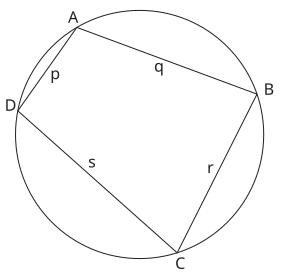
In de meetkunde geeft de formule van Brahmagupta de oppervlakte van een vierhoek, gegeven de lengtes van de zijden en enige van hun hoeken.

Basisvorm

In haar basisvorm geeft de formule van Brahmagupta de oppervlakte van een koordenvierhoek, d.w.z. een vierhoek waarvan de vier punten op een cirkel liggen. Als de zijden lengten a, b, c en d hebben, is de oppervlakte

${\sqrt {(s-a)(s-b)(s-c)(s-d)}}$.

Daarin is s de halve omtrek:

$s={\tfrac {1}{2}}(a+b+c+d)$

De formule van Heron is een speciaal geval voor de oppervlakte van een driehoek.

De bewering dat de oppervlakte van de vierhoek wordt gegeven door de formule van Brahmagupta is gelijkwaardig aan de bewering dat de oppervlakte gelijk is aan

${\tfrac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2}+d^{2})^{2}+8abcd-2(a^{4}+b^{4}+c^{4}+d^{4})}}$

De formule van Brahmagupta kan worden gezien als een formule in halve lengtes van de zijden, maar de formule geeft ook de oppervlakte als een formule in de hoogten vanuit het centrum naar de zijden, hoewel als de vierhoek niet het centrum bevat, de hoogte naar de langste zijde als een negatief getal moet worden opgevat.

Gerelateerde stellingen

• Formule van Heron voor het berekenen van de oppervlakte van een driehoek is het speciale geval, dat men verkrijgt door $d=0$ te nemen.
• De relatie tussen de algemene en uitgebreide vorm van de formule van Brahmagupta is vergelijkbaar met hoe de cosinusregel uitbreidbaar is naar de stelling van Pythagoras

Externe link

• (en) formule van Brahmagupta op MathWorld