Inversie (meetkunde)

P en Q zijn elkaars cirkelinversen.

Twee cirkels (groen en blauw) als elkaars inverse in de rode cirkel.

Een lijn (groen) en cirkel (blauw) door het middelpunt van de inversiecirkel als beeld van elkaar.

Constructie van inversie.

Andere constructie van inverse.

Inversie heeft in de meetkunde twee verschillende betekenissen. Het gaat in beide gevallen om een soort afbeelding.

Er wordt in dit artikel vooral op de inversie ingegaan die synoniem is met cirkelspiegeling. Met deze betekenis is het een soort spiegeling in een cirkel in het platte vlak.

Een puntspiegeling wordt ook een inversie genoemd. Een puntspiegeling beeldt een vector in tegengestelde richting af.

Definities voor de cirkelspiegeling

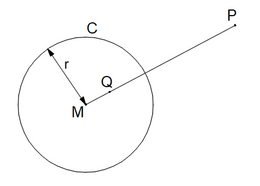
We nemen een cirkel C met middelpunt M en straal r. Gegeven een punt P, dan is de inverse van P in C het punt Q op de halve lijn MP zodat

$MP\cdot MQ=r^{2}.$

• r² heet de macht van inversie,
• M is het centrum van inversie.

Het beeld van een punt onder inversie heet zijn inverse.

Een middencirkel van twee cirkels C₁ en C₂ is een cirkel C die door inversie C₁ en C₂ op elkaar afbeeldt.

Eigenschappen

• De inverse van de inverse van een punt is het punt zelf.
• Inversie beeldt in het algemeen cirkels af op cirkels of lijnen. Deze lijnen zijn op te vatten als ontaarde cirkels, met oneindige straal. In het bijzonder is het beeld van een cirkel door M een lijn, en het beeld van een cirkel niet door M is een cirkel niet door M.
• Het middelpunt van een cirkel, het middelpunt van zijn inverse en M liggen op één lijn, meer specifiek is M een gelijkvormigheidscentrum van de twee cirkels.
• Gegeven de inversie met centrum M en macht p, is het beeld van een cirkel met middelpunt A en straal r, met afstand d tussen M en A, een cirkel met straal $\left|{\frac {pr}{d^{2}-r^{2}}}\right|$ en middelpunt $A+{\frac {p}{d^{2}-r^{2}}}(A-M).$
• Cirkels die C loodrecht snijden zijn invariant onder inversie.
• Inversie behoudt hoeken.
• Als A en B de snijpunten zijn van MP met C, dan liggen (A,B) en (P,Q) harmonisch.

Constructie

• Constructie van de inverse Q van een punt P in het inwendige van C:
  1. Construeer de lijn d door P loodrecht op MP
  2. Snijdt d met C, noem de snijpunten R en R',
  3. Construeer de cirkel door M, R en R',
  4. Het tweede snijpunt van deze cirkel en MP is het gezochte punt Q.

• Constructie van de inverse P van een punt Q in het uitwendige van C:
  1. Construeer de cirkel met diameter MQ,
  2. Snijdt de twee cirkels, noem de snijpunten R en R',
  3. Het snijpunt van RR' en MQ is het gezochte punt P.

• Alternatieve constructie van de inverse:
  1. Neem een punt op de inversiecirkel S1,
  2. Construeer de raaklijn aan S1 door dit punt,
  3. Construeer de middelloodlijn van het gegeven punt (A of B) en het punt op S1,
  4. Snij deze twee lijnen, het snijpunt is het middelpunt van een cirkel S2 loodrecht op S1 door het gegeven punt,
  5. Het tweede snijpunt van de lijn door het inversiecentrum O en het gegeven punt met S2 is de inverse.

• Nog een alternatief voor een constructie van de inverse met enkel passer en liniaal:
  1. Trek een lijn L door het te inverteren punt P en het centrum M
  2. Trek nog een andere lijn door P die de inversiecirkel C op twee plaatsen snijdt, noem de snijpunten S en S´
  3. Draai een cirkel door S rondom een punt op L anders dan M
  4. Trek een lijn door S´ en het tweede snijpunt van deze cirkel met de inversiecirkel
  5. Het snijpunt van deze lijn met de lijn L is de inverse van punt P

• Nog een alternatief voor een constructie van de inverse met enkel passer en liniaal, voor als het middelpunt M van de inversiecirkel niet bekend is:
  1. Trek een lijn door P die de inversiecirkel op twee plaatsen snijdt, maar duidelijk niet een diameter is. Noem de snijpunten U en V
  2. Draai een cirkel om P door U. Noem het andere snijpunt van de twee cirkels W
  3. Trek een lijn P en W. Noem het andere snijpunt met de inversiecirkel X
  4. Het snijpunt van de lijnen door VW resp. UX is de inverse van punt P