Knik (constructieleer)

Het horizontaal verbuigen van spoorstaven (spoorspatting) is een gevolg van knik.

Een knik is een ongecontroleerde, plaatselijke scherpe verbuiging (een plastische vervorming) in een rechte of licht gekromde staaf of balk. Een knik wordt veroorzaakt door een uitwendige kracht en gaat gepaard met verlies van stabiliteit. Bij een knik blijft, in tegenstelling tot bij een breuk, het verband (gedeeltelijk) intact.

Een knik kan bijvoorbeeld ontstaan bij een driepuntsbuigproef.

Sterkteleer[bewerken | brontekst bewerken]

In de constructieleer zijn knik en buiging verschillende vormveranderingen van een belaste kolom. Zij komen nagenoeg altijd samen voor, omdat het praktisch onmogelijk is een kniklast precies boven het midden van een kolom te plaatsen. Onder het kopje eulerknik, wordt een theoretische formule van Euler besproken, waarbij ook gewezen wordt op extra momenten, die nader worden toegelicht. "Knik en buiging" is een bekende uitdrukking in de constructieleer.

Een stalen kolom zal door een niet centraal op die kolom rustende belasting een moment krijgen, dat in de richting werkt van de resultante van die oplegging naar het midden van de kolom. Dat moment zal een geringe boogvormige verbuiging veroorzaken, die door toename van de belasting verandert in een sinusvormige verbuiging. Als de oplegging een constructieonderdeel is dat vast verbonden is met de kolom, is in de regel het moment zo groot, dat het apart moet worden berekend.

Als de belastingveroorzakende resultante zich binnen het doorsnedeoppervlak van de kolom bevindt, is de randspanning door het moment maximaal 3 keer groter dan de gelijkelijk over de doorsnede verdeelde kniklast. De randspanning is dan dus 4 keer groter dan de gelijkelijk verdeelde belasting (M/W + F/A).

Een veiligheidsfactor van 4 (of 1/4) is dus wenselijk bij knikberekeningen waarbij men theoretisch uitgaat van een kniklast midden boven de kolom.

Eulerknik[bewerken | brontekst bewerken]

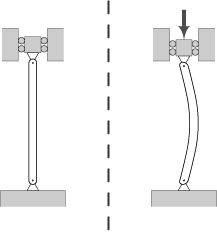
Uitbuigen op druk belaste staaf (beide zijden scharnierend opgelegd)

Eulerknik is het verschijnsel dat optreedt als een staaf zonder imperfecties (een perfect rechte staaf) op zuivere druk (enkel normaalkracht, geen momenten aanwezig) wordt belast totdat de knikgrens wordt overschreden.

Zodra deze grens bereikt is, zal een staaf in een of meer sinusvormige bogen loodrecht op de staafas uitbuigen. Omdat deze vorm van instabiliteit kan leiden tot bezwijken voordat de volledige materiaalcapaciteit bereikt is, zal een gedrukte constructie hierop altijd gecontroleerd moeten worden.

Een staaf zal alleen uitbuigen indien een "kritische belasting" aangebracht wordt. In de 18e eeuw stelde de wiskundige Leonhard Euler een formule op die de maximale belasting bepaalt die een lange, slanke staaf kan dragen zonder te knikken. Deze formule geldt alleen bij elastische uitwijking van de staaf. Dit treedt op boven een bepaalde grensslankheid van de staaf, die afhankelijk is van lengte, doorsnede en materiaal. De precieze grootte van deze kracht wordt bepaald door de oplossing van een differentiaalvergelijking en de randvoorwaarden, en is gelijk aan:

P_{\text{k}}={\frac {\pi ^{2}\cdot E\cdot I}{l_{\text{k}}^{2}}}

Hierin is $E$ de elasticiteitsmodulus, $I$ het oppervlaktetraagheidsmoment en $l_{\text{k}}$ de kniklengte. De kniklengte is de afstand tussen een top en een dal van de momentenfunctie, en hoeft niet gelijk te zijn aan de effectieve lengte van de staaf. In het voorbeeld, waarbij als randvoorwaarden twee scharnieropleggingen zijn aangebracht, is de kniklengte gelijk aan de lengte van de staaf.

Voor het bestaan van eulerknik gebruikte men de hiergenoemde "momentenknik". Daarbij gaat men uit van een onder en boven scharnierende staaf, waarbij in de scharnierpunten gelijke doch tegengestelde momenten werken. Door die momenten ontstaat halverwege de staaflengte een uitbuiging : f = M.L^2 / 8.E.I, waarin M = P x f. In de vergelijking kan dan links en rechts de f weggestreept worden, hetgeen betekent, dat er geen uitbuiging is als geldt:

P={\frac {8\cdot E\cdot I}{L^{2}}}

.

De conclusie is dan gerechtvaardigd om te stellen, dat als P groter wordt er een uitbuiging ontstaat die tot bezwijken toeneemt en als P kleiner wordt de uitbuiging terug wil gaan naar 0 of de kromming die door een gering extern moment is veroorzaakt.

De eulerknikformule is puur theoretisch, als de staaf niet perfect recht is (en dit zal in werkelijkheid altijd zo zijn), of de staaf excentrisch wordt belast, zal de drukspanning in de staaf, samen met de initiële uitbuiging, voor een extra moment zorgen waardoor de staaf vroegtijdig (onder de knikgrens) bezwijkt. In de puur theoretische formule liggen de belasting en het hart van de staaf in een lijn. De drukspanning is dan halverwege de staaf gelijkmatig over de doorsnede verdeeld en er geldt : σk = P/F, waarin F het oppervlak van de doorsnede is. Bij toename van de belasting zal de staaf niet knikken maar in elkaar gedrukt worden. Als de spanning niet gelijkmatig verdeeld is, liggen de belasting en de hart(lijn) van de staaf niet in een lijn en is er sprake van druk en buiging, waarbij de onregelmatig verdeelde drukspanning verandert in knikspanning, waardoor "knik en buiging" ontstaat.

Zie ook[bewerken | brontekst bewerken]