Lognormale verdeling

Lognormale verdeling
Kansdichtheid μ=0
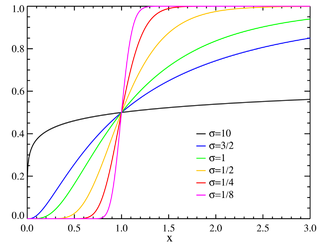
Verdelingsfunctie μ=0
Parameters	$\sigma > 0$ $-\infty < \mu < \infty$
Drager	$[0,+\infty)\!$
Kansdichtheid	$\frac{1}{x\sigma\sqrt{2\pi}}\exp\left[-\frac{\left(\ln(x)-\mu\right)^2}{2\sigma^2}\right]$
Verdelingsfunctie	$\frac{1}{2}+\frac{1}{2} \mathrm{erf}\left[\frac{\ln(x)-\mu}{\sigma\sqrt{2}}\right]$
Verwachtingswaarde	$e^{\mu+\sigma^2/2}$
Mediaan	$e^{\mu}\,$
Modus	$e^{\mu-\sigma^2}$
Variantie	$(e^{\sigma^2}\!\!-1) e^{2\mu+\sigma^2}$
Scheefheid	$(e^{\sigma^2}\!\!+2)\sqrt{e^{\sigma^2}\!\!-1}$
Kurtosis	${e^{4\sigma^2}+2e^{3\sigma^2}+3e^{2\sigma^2}-6}$
Entropie	$\frac{1}{2}+\frac{1}{2}\ln(2\pi\sigma^2) + \mu$
Portaal    Wiskunde

In de kansrekening is de lognormale verdeling de kansverdeling van een stochastische variabele waarvan de logaritme normaal verdeeld is. Als de stochastische variabele Y normaal verdeeld is, heeft de stochastische variabele X = e^Y dus een lognormale verdeling. In de statistiek wordt een lognormale verdeling gebruikt om een variabele te modelleren die gezien kan worden als het multiplicatieve resultaat van een aantal kleine, onafhankelijke factoren.

Definitie

De lognormale verdeling is de kansverdeling met als kansdichtheid, gedefinieerd voor x > 0,

$f(x;\mu,\sigma) = \frac{1}{x \sigma \sqrt{2 \pi}}\ e^{-\frac12\left(\frac{\ln (x) - \mu}{\sigma}\right)^2}.$

Hierin stellen de parameters μ en σ respectievelijk de verwachtingswaarde en de standaardafwijking van de natuurlijke logaritme van de betrokken variabele voor. De verdelingsfunctie is

$\frac{1}{2}+\frac{1}{2} \mathrm{erf}\left[\frac{\ln(x)-\mu}{\sigma\sqrt{2}}\right]$

Hoewel alle momenten bestaan en gegeven worden door

$\mu_k=e^{k\mu+k^2\sigma^2/2}$,

bestaat de moment-voortbrengende functie zelf niet.

Eigenschappen

De verwachtingswaarde is gelijk aan

$\mathrm{E}(X) = e^{\mu + \sigma^2/2}.\,\!$

De variantie is

$\mathrm{var}(X) = (e^{\sigma^2} - 1) e^{2\mu + \sigma^2}\,\!$

Hierin is X een toevalsvariabele die lognormaal verdeeld is.

Overige eigenschappen, zoals modus, mediaan en scheefheid, staan in de tabel rechtboven.

Omdat de lognormale verdeling gebruikt wordt in situaties met een multiplicatief karakter, is het zinvol om naar het geometrisch gemiddelde te kijken. Dit is gelijk aan $e^{\mu}\,\!$. De geometrische standaarddeviatie is $e^{\sigma}\,\!$. Deze eigenschappen kunnen gebruikt worden om betrouwbaarheidsintervallen te creëren:

Grens betrouwbaarheidsinterval	Waarde
-3σ ondergrens	$\exp(\mu) \exp(-3\sigma)\,\!$
-2σ ondergrens	$\exp(\mu) \exp(-2\sigma)\,\!$
-1σ ondergrens	$\exp(\mu) \exp(-\sigma)\,\!$
1σ bovengrens	$\exp(\mu) \exp(\sigma)\,\!$
2σ bovengrens	$\exp(\mu) \exp(2\sigma)\,\!$
3σ bovengrens	$\exp(\mu) \exp(3\sigma)\,\!$

Gerelateerde verdelingen

• Als $X \sim N(\mu, \sigma^2)$ dan $\exp(X) \sim \operatorname{Log-N}(\mu, \sigma^2)$.
• Als $X_m \sim \operatorname {Log-N} (\mu, \sigma_m^2), \ m = 1,\dots, n$ onafhankelijke lognormaal verdeelde stochasten, met dezelfde waarde μ, zijn en $Y = \prod_{m=1}^n X_m$, dan volgt Y een lognormale verdeling: $Y \sim \operatorname {Log-N} \left( n\mu, \sum _{m=1}^n \sigma_m^2 \right)$.