Spiraal van Theodorus

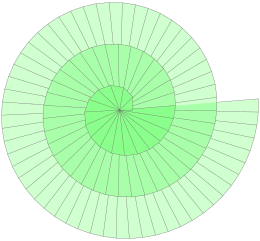
De spiraal van Theodorus is een spiraal die ontstaat door rechthoekige driehoeken aan elkaar te plakken. Men begint met een rechthoekige driehoek met rechthoekzijden van lengte 1. Vervolgens plakt men aan de hypotenusa een zijde van lengte 1 onder een rechte hoek, en vormt zo een tweede rechthoekige driehoek. Dit proces herhaalt men en zo ontstaat de spiraal van Theodorus.
De hypotenusa's van de rechthoekige driehoeken in deze spiraal vormen de rij , , , ... Dit volgt meteen uit de stelling van Pythagoras.
De eigenlijke spiraal wordt gevormd door de telkens aangeplakte rechthoekszijden van lengte 1. De spiraal nadert asymptotisch naar een Archimedes-spiraal met een windingsbreedte van π. Geen enkele van de hypotenusa's in de spiraal valt samen met een vorige hypotenusa.
De spiraal van Theodorus is vernoemd naar Theodorus van Cyrene die de spiraal als eerste construeerde. Hij hield op bij de driehoek met hypotenusa , vermoedelijk[bron?] omdat dat de laatste is die niet een vorige driehoek overlapt.




