Swift-Hohenbergvergelijking
De Swift-Hohenbergvergelijking is een niet-lineaire partiële differentiaalvergelijking met als algemene vorm
Hierin is of een reële functie van plaats en tijd, de laplace-operator, een reële bifurcatieparameter en een niet-lineaire functie van . De "kanonieke" Swift-Hohenbergvergelijking heeft , en is genoemd naar Jack Swift en Pierre Hohenberg, die deze vergelijking in 1977 voorstelden.[1]
Oorsprong[bewerken | brontekst bewerken]
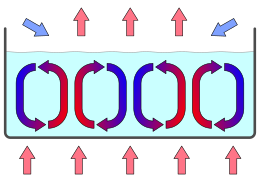
De vergelijking is een beschrijving voor veel zogeheten patroonvormende systemen, fysische of chemische systemen waarin een homogene toestand "spontaan" overgaat in een toestand met een duidelijk patroon, waarbij het patroon een gevolg is van zelforganisatie en niet van buitenaf is opgelegd. Een bekend voorbeeld, waarvoor de Swift-Hohenbergvergelijking met een benadering is, is de Rayleigh-Bénardconvectie[1]: een stilstaande vloeistof die in een afgesloten vat van onder wordt verhit, gaat convectie vertonen als het temperatuurverschil tussen boven- en onderkant van het vat voldoende groot is. Als het vat relatief plat is, zal die in de vorm van duidelijke convectierollen gebeuren. De Swift-Hohenbergvergelijking geeft een benaderde beschrijving van dit proces.
Triviale oplossing en lineaire stabiliteit[bewerken | brontekst bewerken]
Het is duidelijk dat (we beschouwen nu het (1+1)-dimensionale geval) altijd een oplossing van deze vergelijking is. Een belangrijke vraag is dan of deze oplossing stabiel is. Met "stabiel" wordt hier de zogeheten lineaire stabiliteit bedoeld: als het systeem in deze toestand is, wat gebeurt er dan wanneer een infinitesimaal kleine verstoring wordt aangebracht? Als alle mogelijke verstoringen steeds kleiner worden, is het systeem lineair stabiel; als er verstoringen zijn die (aanvankelijk) groeien, is het systeem lineair instabiel. Het blijkt dat voor het systeem lineair stabiel is. Voor is het systeem instabiel: wanneer men een willekeurig kleine verstoring van de vorm neemt, blijkt deze te groeien. In het Rayleigh-Bénardsysteem wordt deze parameter bepaald door een balans tussen de viscositeit van de vloeistof, die de stroming "tegenwerkt", en het lichter zijn van de warmere vloeistof, waardoor deze van onder naar boven "wil" stromen.[2]
Bifurcatie-analyse[bewerken | brontekst bewerken]
In geval van lineaire instabiliteit van een evenwicht, treedt doorgaans een bifurcatie op: op dit punt verschijnen nieuwe evenwicht, dat wil zeggen, nieuwe stationaire oplossingen van de vergelijking. In dit geval blijken deze oplossingen te bestaan voor , bij benadering sinusoïde te zijn en stabiel te zijn. In wezen zijn er oneindig veel van deze oplossingen: er is een familie van oplossingen
- voor golfgetal
waarbij de amplitudo afhangt van en . Als we ons beperken tot de oplossing met , die het eerst verschijnt zodra , kunnen we deze bifurcatie beschouwen als een superkritische hooivorkbifurcatie.
Voor twee ruimtelijke dimensies kan men de oplossingen schrijven als , waarbij de golfvector is, en .
Patronen[bewerken | brontekst bewerken]

De sinusoïde oplossingen die hierboven worden beschreven, komen overeen met rollen in de vloeistof, en hun gedrag nabij de overgang of bifurcatie is goed begrepen. Voor bepaalde waarden van en kunnen deze rollen zelf weer instabiel worden. Men spreekt dan van secundaire instabiliteiten. In de "gewone" Swift-Hohenbergvergelijking in één dimensie gebeurt dit via de zogeheten Eckhausinstabiliteit.
Een rijkere dynamica verkrijgt men door te kijken naar tweedimensionale systemen of door andere termen toe te voegen aan de niet-lineariteit. Met een kleine kwadratische term erbij, zodat , verkrijgt men in twee dimensies bijvoorbeeld zeshoekige patronen. Wanneer men neemt, heeft men voor in wezen de Kuramoto-Sivashinskyvergelijking, die chaotisch gedrag kan vertonen.
Amplitudevergelijkingen[bewerken | brontekst bewerken]

Veel van het gedrag van deze vergelijking voor kleine positieve kan goed worden beschreven door de oplossingen te beschouwen als gemoduleerde sinusoïden: we beschrijven de oplossingen als het product van een golf met korte golflengte en een amplitude die op langere lengteschaal en langzame tijdsschaal varieert. Vervolgens leiden we een vergelijking af die deze amplitude beschrijft in plaats van het oorspronkelijke systeem. Met een dergelijke amplitudevergelijking kan men relatief eenvoudig veel van de fenomenologie van de vergelijking rond het bifurcatiepunt beschrijven.[3] De Swift-Hohenbergvergelijking kan haast als een paradigma worden beschouwd voor de toepassing van amplitudevergelijkingen.
Referenties[bewerken | brontekst bewerken]
- ↑ a b Jack B. Swift en Pierre C. Hohenberg, Physical Review A, vol. 15 (1977), p. 319
- ↑ Paul Manneville, Instabilities, Chaos and Turbulence, Imperial College Press, Londen, 2004
- ↑ Michael C. Cross en Pierre C. Hohenberg, Pattern formation outside of equilibrium, Reviews of Modern Physics, vol. 65 (1993) pp. 851–1112
Externe link[bewerken | brontekst bewerken]
- Enkele instructieve Java-demonstratie-applets op de website van Michael Cross














![{\displaystyle k\in [1-\varepsilon ,1+\varepsilon ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78702eef3e23394a5e5f43b5f4d7dfc715c37f86)









