Scheidingsaxioma

Aan een topologische ruimte worden soms aanvullende voorwaarden opgelegd om sterkere eigenschappen te kunnen bewijzen. De scheidingsaxioma's zijn dergelijke voorwaarden, die alle te maken hebben met de mogelijkheid of onmogelijkheid, verschillende elementen van de verzameling $X$ te onderscheiden door middel van open verzamelingen.

Kolmogorov-ruimte: T₀

Een topologische ruimte heet een Kolmogorov-ruimte, ook $T_{0}$-ruimte of kortweg $T_{0}$, als er voor ieder puntenpaar een open verzameling bestaat die precies één van de twee punten bevat. Met andere woorden: alle punten kunnen van elkaar worden gescheiden door open verzamelingen.

De meeste praktische elementaire voorbeelden van topologische ruimten zijn $T_{0}$, dus het is interessanter een tegenvoorbeeld te geven. De indiscrete topologie op een verzameling $X$ heeft slechts twee open verzamelingen: de lege verzameling en $X$ zelf. Als $X$ minstens twee elementen bevat, dan is de indiscrete topologie niet $T_{0}$.

Een pseudometrische ruimte die geen metrische ruimte is, geeft aanleiding tot een topologie die niet $T_{0}$ is. Twee verschillende punten met onderlinge afstand 0 kunnen immers niet gescheiden worden door open verzamelingen.

Fréchet-ruimte: T1

Een topologische ruimte heet Fréchet (niet "Fréchetruimte", dat is een begrip uit de functionaalanalyse), ook $T_{1}$-ruimte of kortweg $T_{1}$, als er voor ieder puntenpaar $(x,y)$ een open verzameling bestaat die $x$ bevat maar niet $y$, en een open verzameling die $y$ bevat maar niet $x$. Dit is gelijkwaardig met de eis dat alle singletons gesloten verzamelingen zijn.

Het is gemakkelijk te zien dat $T_{1}$ minstens even sterk is als $T_{0}$: elke $T_{1}$-ruimte is een $T_{0}$-ruimte. Het omgekeerde is niet waar: er zijn $T_{0}$-ruimten die niet $T_{1}$ zijn.

Een niet-triviaal voorbeeld van dit laatste vormt de Zariski-topologie op het spectrum van een commutatieve ring (zie de voorbeelden bij de definitie van een topologische ruimte). Deze is altijd $T_{0}$, maar ze is pas $T_{1}$ als alle priemidealen van de ring maximaal zijn.

Hausdorff-ruimte: T2

Een topologische ruimte heet Hausdorff-ruimte, ook $T_{2}$-ruimte of kortweg $T_{2}$, als er voor ieder puntenpaar $(x,y)$ een disjunct paar open verzamelingen $(F,G)$ bestaat zodat elk van beide verzamelingen precies één van de twee punten bevat. Dit is gelijkwaardig met de eis dat de diagonaalverzameling $\{(x,x)|x\in X\}$ (de verzameling identieke koppels van $X$) een gesloten deel is van het Cartesisch product $X\times X$, uitgerust met de producttopologie.

Het is opnieuw gemakkelijk te zien dat $T_{2}$ minstens even sterk is als $T_{1}$. En ook hier bestaan er tegenvoorbeelden voor de omgekeerde bewering. De cofiniete topologie (zie voorbeelden topologische ruimte) is altijd $T_{1}$, maar ze is slechts $T_{2}$ op een eindige ruimte.

Aan deze soort topologische ruimten is het afzonderlijke artikel Hausdorff-ruimte gewijd.

Reguliere ruimte: T3

Voor elke gesloten verzameling F en elk punt x buiten F bestaat er een disjunct stel omgevingen.

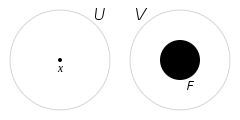
Een topologische ruimte heet regulier, ook $T_{3}$-ruimte of kortweg $T_{3}$, als aan de volgende twee voorwaarden voldaan is:

1. de ruimte is $T_{1}$
2. voor elk punt x en elke gesloten verzameling F die x niet bevat, bestaat er een disjunct paar open verzamelingen (U,V) zodat x tot U behoort, en F een deel is van V.

Als een ruimte $T_{3}$ is, dan is ze ook $T_{2}$. Immers, uit de eerste voorwaarde volgt dat alle singletons gesloten zijn. Maar door de tweede voorwaarde toe te passen op het bijzondere geval van de gesloten verzameling $F=\{y\}$ volgt de $T_{2}$-voorwaarde.

Er bestaan voorbeelden van niet-reguliere Hausdorff-ruimten.

Normale ruimte: T4

Elk paar disjuncte gesloten verzamelingen {E,F} heeft een disjunct stel omgevingen.

Een topologische ruimte heet normaal, ook $T_{4}$-ruimte of kortweg $T_{4}$, als aan de volgende twee voorwaarden voldaan is:

1. de ruimte is $T_{1}$
2. voor elk paar disjuncte gesloten verzamelingen (E,F) bestaat er een disjunct paar open verzamelingen (U,V) zodat E een deel is van U, en F een deel is van V.

Als een ruimte $T_{4}$ is, dan is ze ook $T_{3}$. Immers, de eerste voorwaarde is in beide gevallen identiek. En uit de eerste voorwaarde volgt dat alle singletons gesloten zijn. Maar door de tweede voorwaarde toe te passen op het bijzondere geval van de gesloten verzameling E={x} volgt de tweede $T_{3}$-voorwaarde.

Er bestaan voorbeelden van niet-normale, reguliere ruimten.

$T_{3.5}$

Pavel Urysohn bewees dat in een normale ruimte steeds de volgende stelling geldt: voor ieder punt $x$ en voor iedere gesloten verzameling $G$ waar $x$ niet toe behoort, bestaat er een continue afbeelding van de hele ruimte $X$ naar het gesloten interval $[0,1]$ die $x$ afbeeldt op $0$, en $G$ op $\{1\}$.

Niet alle ruimten waarin bovenstaande stelling geldt, zijn normaal. We noemen dergelijke ruimten Tychonov-ruimten of volledig reguliere ruimten. De benaming $T_{3.5}$ voor deze ruimten volgt uit het feit (niet moeilijk te bewijzen) dat elke Tychonov-ruimte regulier is, dus $T_{3.5}$ is minstens even sterk als $T_{3}$.

Metrische ruimten zijn normaal, en voldoen dus meteen aan alle scheidingsaxioma's. Niet alle normale topologische ruimten kunnen verkregen worden uit een metriek; om metriseerbaarheid te garanderen moeten ook aftelbaarheidseigenschappen voldaan zijn (zie aftelbaarheidsaxioma's).