Mandelbrotverzameling

Mandelbrotverzameling.

De mandelbrotverzameling in het complexe vlak

De baan van het getal –2
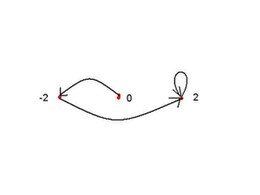
–2 blijkt een begrensde rij op te leveren.

Door kleuren aan te brengen die overeenkomen met de snelheid waarmee de rij divergeert, ontstaat een kleurrijke figuur.

detail

De mandelbrotverzameling is een fractal die een belangrijke rol speelt in de chaostheorie. De verzameling is genoemd naar Benoît Mandelbrot, een Pools-Franse wiskundige, die de fractal in 1980 voor het eerst met de behulp van een computer onderzocht. De verzameling werd echter al in 1905 onderzocht door Pierre Fatou, een Franse wiskundige, die zich specialiseerde in de studie van recursieve vergelijkingen.

Buiten de chaostheorie staat de mandelbrotverzameling vooral bekend om zijn esthetische eigenschappen, en is daarom vaak het onderwerp van recreatieve wiskunde en inleidende cursussen in fractals.

De mandelbulb komt met de mandelbrotverzameling voor drie dimensies overeen.

Uitleg

De mandelbrotverzameling is een verzameling van complexe getallen en ontstaat door herhaaldelijk op de complexe getallen een bepaalde wiskundige bewerking uit te voeren. Deze verzameling wordt dus aan de hand van een differentievergelijking bepaald. Voor ieder complex getal $c$ wordt dezelfde bewerking herhaald, waarbij er een rij complexe getallen $(z_{n})$ wordt gecreëerd, volgens: $z_{n+1}=z_{n}^{2}+c$ met als startwaarde $z_{0}=0$.

Voorbeeld
Neem het complexe getal $c=2+{\tfrac {1}{2}}i$. Omdat $z_{0}=0$, is $z_{1}=c$ en $z_{2}=c^{2}+c$. $c^{2}=(2+{\tfrac {1}{2}}i)^{2}=2^{2}+2\cdot 2\cdot {\tfrac {1}{2}}i+({\tfrac {1}{2}})^{2}\cdot i^{2}$
Tel hierbij $c$ nog een keer op: $z_{2}=\left({\tfrac {15}{4}}+2i\right)+(2+{\tfrac {1}{2}}i)=5{,}75+2{,}5i$ Dit is de eerste stap in het iteratieproces.

Als deze bewerking voor elk complex getal voortdurend wordt herhaald, blijken er twee soorten complexe getallen te bestaan. Er zijn complexe getallen die bij de genoemde bewerkingen een begrensde rij opleveren. En er zijn complexe getallen die bij de gegeven bewerkingen een onbegrensde rij opleveren: de uitkomsten worden steeds groter naarmate de bewerking vaker wordt herhaald. Dit is onder meer het geval bij het bovenstaande voorbeeld van het getal $2+{\tfrac {1}{2}}i$.

De mandelbrotverzameling bestaat uit alle getallen die bij bovenstaande bewerkingen een begrensde rij blijken op te leveren. Hoe vaak de bewerking ook wordt herhaald, de uitkomsten blijven binnen bepaalde waarden. De gehele mandelbrotverzameling valt binnen de cirkel met straal 2 en het middelpunt in de oorsprong. De getallen die leiden tot een onbegrensde rij, kunnen nog binnen deze cirkel liggen, maar vallen allemaal per definitie buiten de mandelbrotverzameling.

Een punt dat tijdens het herhalen van de bewerkingen na verloop van tijd telkens opnieuw uitkomt bij dezelfde waarde(n), wordt een Misiurewicz-punt genoemd. Binnen de mandelbrotverzameling liggen er oneindig veel van.

Kleurgebruik

In afbeeldingen wordt de mandelbrotverzameling vaak met een zwarte kleur weergegeven, en de getallen die buiten de verzameling vallen met een andere kleur. Ook wordt een groot aantal kleuren gebruikt, die geleidelijk in elkaar overgaan. Meestal worden de kleuren zo gekozen dat zij een indicatie zijn van het aantal iteraties die nodig zijn voordat een onbegrensde rij een waarde oplevert die buiten de cirkel valt waarbinnen zich de mandelbrotverzameling bevindt. Als ingezoomd wordt op de randen van de afbeelding van de mandelbrotverzameling, worden al gauw locaties zichtbaar met punten die honderden iteraties behoeven, voordat vastgesteld is dat ze onbegrensd zijn. Als er bijvoorbeeld 256 kleuren gebruikt worden, beginnend met een donkerblauwe kleur (voor de punten die meteen buiten de cirkel liggen), wordt die donkerblauwe kleur na 256 en na 512 iteraties opnieuw gebruikt (voor punten die na 256 of na 512 iteraties buiten de cirkel komen te liggen).

Wiskundige beschrijving

De mandelbrotverzameling wordt formeel gedefinieerd met behulp van de klasse complexe tweedegraadspolynomen:

$f_{c}(z)=z^{2}+c$

De verzameling bestaat uit de punten $c$ in het complexe vlak, waarvoor de rij

$(0,f_{c}(0),f_{c}(f_{c}(0)),f_{c}(f_{c}(f_{c}(0))),\ldots \ )\ =$

$(0\ ,\ c,\ c^{2}+c\ ,\ (c^{2}+c)^{2}+c\ ,\ldots \ )$

niet wegloopt naar oneindig.

Men onderzoekt de mandelbrotverzameling met behulp van de recursieve relatie:

$z_{0}=0$

$z_{n+1}=z_{n}^{2}+c$

De rij kan als volgt worden uitgeschreven:

$c=a+bi$

$z_{0}=0$

$z_{1}=z_{0}^{2}+c=c=a+bi$

$z_{2}=z_{1}^{2}+c=(a+bi)^{2}+a+bi=a^{2}-b^{2}+a+(2ab+b)i$

$z_{3}=z_{2}^{2}+c=\ldots$

enz.

Gesplitst in het reële- en imaginaire deel, respectievelijk de x- en y-coördinaten van het complexe vlak, met:

$z_{n}=x_{n}+y_{n}i$

wordt dit:

$x_{n+1}=x_{n}^{2}-y_{n}^{2}+a$

en

$y_{n+1}=2x_{n}y_{n}+b$

Beschrijving van de fractal

De mandelbrotverzameling is een samenhangende verzameling die kan worden verdeeld in een oneindige verzameling van figuren: de grootste figuur in het centrum is een cardioïde. Er is een aftelbaar oneindig aantal bijna-cirkels, waarvan de diameter asymptotisch naar nul nadert. De enige volledige cirkel bevindt zich direct links van de cardioïde. Elk van de bijna-cirkels heeft op zijn beurt een eigen aftelbaar oneindig aantal kleinere cirkels om zich heen, die zich vanuit de cirkel vertakken. Deze vertakking zet zich oneindig voort, en aldus vormt zich een fractal.

Bewezen kan worden dat alle punten binnen deze fractal aangrenzende punten zijn. Deze fractal is dus samenhangend ofwel gesloten, net als de juliafractals waaruit het object is opgebouwd.

Voorbeelden

Ingezoomd op een deel van de mandelbrotverzameling	Ingezoomd op een deel van de mandelbrotverzameling

• (en) R Penrose. The Emperor's New Mind, 1999. ISBN 0-19-851973-7, hoofdstuk 3
• Dit artikel of een eerdere versie ervan is een (gedeeltelijke) vertaling van het artikel Mandelbrot set op de Engelstalige Wikipedia, dat onder de licentie Creative Commons Naamsvermelding/Gelijk delen valt. Zie de bewerkingsgeschiedenis aldaar.