Z-score

Zie Z-score (doorverwijspagina) voor andere betekenissen van Z-score.

Z-score aangegeven op een normale verdeling

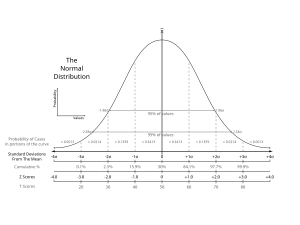
De Z-score of gestandaardiseerde vorm van een stochastische variabele $X$ met verwachting $\mu$ en standaardafwijking $\sigma$ is het verschil van $X$ en $\mu$, uitgedrukt in eenheden van de standaardafwijking:

$Z={\frac {X-\mu }{\sigma }}$

De Z-score betekent een gestandaardiseerde waarde die zich met andere Z-scores laat vergelijken. Een Z-score gelijk aan 2 betekent dat de stochastische variabele $X$ zelf een waarde aanneemt die twee keer voorbij de standaardafwijking ervan ligt. Hoe groot de Z-score is hangt van de stochastische variabele af.

Op basis van de ongelijkheid van Tsjebysjev kan worden afgeleid dat Z-scores van ± 3 en meer zeldzaam zijn. Ongeacht de kansverdeling is de kans hierop hooguit 1/9. Voor de meeste kansverdelingen is deze kans overigens kleiner, zo is voor de normale verdeling de kans op een Z-score van 3 kleiner dan 0,002.

Eigenschappen

• De verwachting van de Z-score is 0 en de standaardafwijking is gelijk aan 1. Als $X$ normaal verdeeld is, is $Z$ standaardnormaal verdeeld.

• Z-scores maken het in bepaalde gevallen mogelijk om steekproeven uit verschillende populaties op een zinvolle manier met elkaar te vergelijken.

• Als de verwachtingswaarde en de standaardafwijking onbekend zijn, wordt voor de uitkomst $x$ van een steekproef als Z-score berekend:

$z={\frac {x-{\bar {x}}}{s}}$

waarin ${\bar {x}}$ het steekproefgemiddelde is en $s$ de steekproefstandaardafwijking.