Marching cubes
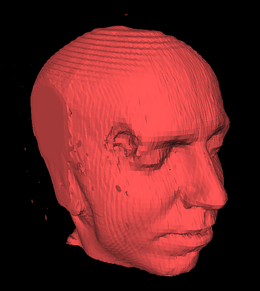

Marching cubes is een algoritme voor volumerendering bij computergraphics. Het algoritme geeft een driedimensionaal object weer als een verzameling verbonden polygonen (meestal driehoekjes). Het algoritme is voor het eerst gepubliceerd in 1987 door William E. Lorensen en Harvey E. Cline.
Algoritme[bewerken | brontekst bewerken]
Werking[bewerken | brontekst bewerken]
Men moet ervan uitgaan dat een 3D object opgedeeld is in een driedimensionaal raster met vele cellen. Het algoritme bouwt nu een mesh op van het 3D object bestaande uit een grote hoeveelheid driehoekjes. Hiertoe worden in eerste instantie alle cellen die aan de buitenkant van het object liggen, gemarkeerd. Voor iedere "buitencel", zal nu een of meer driehoekjes getekend worden.
Het belangrijkste werk van het algoritme is om te bepalen hoeveel driekhoekjes per cel getekend moeten worden, welke vorm en welke oriëntatie ten opzichte van de kijker de driehoekjes krijgen. Hiertoe stelt men een cel voor als een kubus (marching cube). Deze kubus wordt doorsneden door een deel van het 3D object. Het snijvlak dat het 3D object creëert in de marching cube, wordt opgebouwd uit enkele driehoekjes. Eenvoudig gezegd zal het algoritme het snijvlak vormen door de snijpunten van het snijvlak met de kubus te verschuiven langs de zijden van de kubus, zodat de driehoekjes waaruit het snijvlak is opgebouwd de juiste vorm krijgen. De vorm van het snijvlak wordt gedefinieerd als een verzameling punten. De oriëntatie van het snijvlak wordt bepaald door de normaalvector. De snijpunten en de oriëntatie worden opgeslagen, alvorens naar de volgende marching cube te gaan.
Omdat gebruikgemaakt wordt van eenvoudige polygonen, kan de grafische hardware hier gemakkelijk mee overweg en zal het 3D object snel kunnen worden weergegeven.
Een kubus doorsnijden[bewerken | brontekst bewerken]
Men kan op vele manieren vlakken aangeven die een kubus doorsnijden, waarbij bepaalde hoekpunten van de kubus aan de "binnenkant" of aan de "buitenkant" van de doorsnede liggen. Als bekend is hoeveel en welke hoekpunten van een kubus binnen, cq. buiten een doorsnede van de kubus liggen, is eenvoudig na te gaan welke snijvlakken hiervoor verantwoordelijk zijn. Te berekenen is dat er 256 mogelijkheden om doorsnedes te maken van een kubus, waarbij een gegeven aantal hoekpunten aan de "binnenkant" of aan de "buitenkant" van de doorsnede liggen. Sterker nog, door gebruik te maken van de symmetrie van de kubus, kunnen 15 gevallen onderscheiden worden, die alle 256 doorsnedes kunnen vormen. Deze gevallen kan men opslaan in een zgn. "triangle lookup table" (TLT). Wanneer nu bekend is hoeveel en welke knopen er nu aan de buitenkant van een kubus liggen, kan via de TLT snel het bijhorende doorsnede geval bepalen.
Proces[bewerken | brontekst bewerken]
Voor iedere cel in het 3D object wordt het volgende gedaan:
- Kubus bouwen: Stel een denkbeeldige kubus samen uit 4 datapunten uit laag k en 4 datapunten uit laag k+1 van het 3D object. De 8 datapunten functioneren als de 8 knopen van een kubus (v1...v8).
- Hoekpunten classificeren: Het 3D object zal deze denkbeeldige kubus doorsnijden. Bepaal welke hoekpunten van de denkbeeldige kubus binnen of buiten het 3D object vallen.
- Index berekenen: Creëer een index tussen 0 en 255 (1 byte). Iedere bit in de byte stelt een hoekpunt voor. Wanneer een hoekpunt buiten het 3D object valt, zoals bepaald in stap 2, zal de betrokken bit '1' worden, anders '0'.
- Zijden bepalen: Via de index kan uit de TLT een snijvlak gekozen worden. Ieder snijvlak is samengesteld uit een of meer driehoeken.
- Snijpunten van het snijvlak bepalen via interpolatie: De exacte snijpunten van de doorsnee met de denkbeeldige kubus worden bepaald via interpoleren met de hoekpunten van de denkbeeldige kubus.
- Normaalvectoren berekenen en interpoleren: Voor iedere zijde van de denkbeeldige kubus wordt een normaalvector berekend. Interpoleer nu de normaalvectoren van de snijpunten via lineaire interpolatie tussen de normaalvectoren van de hoekpunten van de kubus.
