Bisectie
Bisectie (uit het Latijn: 'in tweeën snijden') of binair zoeken is een methode om in een verzameling een element te vinden dat aan een bepaald criterium moet voldoen, door de af te zoeken deelverzameling van mogelijke waarden steeds te halveren.
De methode werkt alleen als snel kan worden vastgesteld of het gezochte element zich in de ene helft of in de andere helft van de nog mogelijke waarden bevindt. In de praktijk betekent dat meestal dat de verzameling geordend moet zijn.
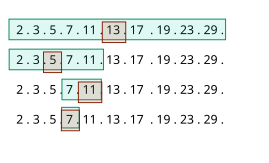
Voorbeeld[bewerken | brontekst bewerken]
Gezocht wordt waar in de geordendede getallenrij zich het element 7 bevindt. Vergelijk het element ongeveer halverwege de rij met 7. Aangezien 7 kleiner is dan 13 moet 7 in het linkerdeel van de rij gezocht worden, anders in het rechterdeel. Uit het linkerdeel wordt het element halverwege, , weer vergeleken met 7. Omdat 5 kleiner is dan 7, ligt 7 dus kennelijk rechts van 7, dus bij de elementen en . Vergelijk nog met 7; , dus 7 ligt links van , dus .
Binair zoeken is de gebruikelijke manier om iets in een woordenboek op te zoeken. Men opent het boek ongeveer in het midden en ziet dan of het gezochte woord in de eerste of tweede helft van het boek moet worden gezocht. In die helft wordt verder gezocht. In de praktijk weet men meteen al ongeveer in welk deel van het boek gezocht moet worden: begint het gezochte woord met een A, dan begint men niet in het midden van het boek. Dat maakt de procedure nog efficiënter - zie hieronder bij #Doelmatigheid.
Implementatie in C++[bewerken | brontekst bewerken]
Recursief[bewerken | brontekst bewerken]
Het volgende fragment van een C++-programma implementeert een recursief bisectie-algoritme:
#include <iostream>
using namespace std;
bool binair_zoeken_rec(int* waarden, int zoek, int l, int r){
if(l==r){
// binair zoeken beperkt zich tot 1 cel, plaats waar het gezochte element verwacht wordt.
return waarden[l] == zoek;
}else{
// bepaal het midden tussen de linkse (l) en rechtse (r) grens
int m = (l+r)/2; // deling van 2 integers blijft int, naar beneden afgerond: 7/2 = 3
if(waarden[m] < zoek){
// zoek in het rechterdeel verder [m+1 , r]
return binair_zoeken_rec(waarden, zoek, m+1,r);
}else{
// zoek in het linkerdeel verder [l, m]
return binair_zoeken_rec(waarden, zoek, l, m);
}
}
}
bool binair_zoeken(int* waarden, int aant, int zoek){
// start de recursie op, met:
// l: linker grens van onze tabel = 0
// r: rechter grens van onze tabel = aantal elementen -1
// zoek: de gezochte waarde
return binair_zoeken_rec(waarden, zoek, 0, aant-1);
}
int main(int argc, const char * argv[]){
int waarden[] = {9,13,17,19,25,26,29,40};
// zoek aanwezige waarde op, bijvoorbeeld 13
cout << (binair_zoeken(waarden, 8, 13) ? "aanwezig" : "afwezig") << endl;
// zoek afwezige waarde op, bijvoorbeeld 16
cout << (binair_zoeken(waarden, 8, 16) ? "aanwezig" : "afwezig") << endl;
}
Lineair[bewerken | brontekst bewerken]
Het volgende fragment implementeert een lineair bisectie-algoritme:
bool ArrayList::find(
char* sFind, // gezochte string
char** aStr, // verzameling strings waarin te zoeken
int nNItems, // aantal strings in de verzameling
int* piInsert // te retourneren invoegpositie
){
/* Deze methode gebruikt bisectie: deelt het te doorzoeken stuk
* steeds in tweeën en beoordeelt steeds een zijde
* van het nieuwe snijvlak. */
int iL= 0;
int iR= nNItems;
int nSpan= iR -iL;
bool bSearch= (nSpan > 0);
int iN= iL +nSpan/2;
bool bFound= false;
while (bSearch){
char* sN= aStr[iN];
int nCmp= strcmp(sFind,sN);
if(nCmp > 0){
/* gezochte string zit in of net rechts naast het rechter stuk */
iL= iN;
} else if (nCmp < 0){
/* gezochte string zit in of net links naast het linker stuk */
iR= iN;
} else{
bFound= true;
break;
}
if (nSpan==1){
if(nCmp > 0){
iN= iR;
} else{
iN= iL;
}
break; // niet gevonden; invoegpositie wel
}
nSpan= iR -iL;
iN= iL +nSpan/2;
} // einde zoeklus
*piInsert= iN; // invoegpositie of positie van de gevonden string
return bFound; // indien false: iN is de invoegpositie, anders de positie van de gevonden string
}
Toepassing op wiskundige functies[bewerken | brontekst bewerken]
Laat een monotoon stijgende functie zijn. Om de waarde van bij een gegeven te vinden is nu bisectie te gebruiken om te benaderen.
Het bovenstaande programmafragment zou als voorbeeld kunnen dienen, met de volgende aantekeningen:
char* sFind: de gegeven waarde a;char** aStr: het functievoorschrift;int nNItems:iLeniR, een schatting van het gebied waar x ligt, als drijvende-kommagetallen;- char* sN= aStr[iN]: berekening van een functiewaarde voor een benadering van x;
if (nSpan==1): test of de gewenste nauwkeurigheid is gehaald.
De 'invoegpositie' is nu de benadering, met een fout ter grootte van (iR - iL).
Doelmatigheid[bewerken | brontekst bewerken]
Bij het benaderen van een functiewaarde wordt de fout bij elke stap de helft kleiner, dat wil zeggen dat we één decimaal verkrijgen per (ruim) drie cycli (drie decimalen per 10 cycli). Bij toepassing op discrete waarden zijn 1000 getallen te doorzoeken in 10 cycli, 1.000.000 in 20 enzovoorts. Het aantal stappen tot de gewenste nauwkeurigheid is met bisectie van tevoren bekend. De worst-case-complexiteitsgraad van de bisectie is logaritmisch, in grote-O-notatie.
Hoewel bisectie betrouwbaar en eenvoudig is, zijn er methoden die in veel gevallen beter werken, vooral voor de toepassing op wiskundige functies. Zulke methodes maken gebruik van (een schatting van) de richtingscoëfficiënt op of rond het laatst gevonden punt. Bij functies zonder sprongen en knikken wijst die waarde ongeveer in de richting van het gezochte punt, zodat de volgende benadering gemiddeld genomen beter is dan met bisectie het geval zou zijn geweest. Voorbeelden zijn de methode van Newton-Raphson en regula falsi.











