Stelling van De Moivre-Laplace

Als n steeds groter wordt zal de vorm van de binomiaalverdeling steeds meer op een gladde normale verdeling gaan lijken.

De stelling van De Moivre-Laplace, is een stelling in de kansrekening die stelt dat de binomiale verdeling met parameters $n$ en $p$ voor grote waarden van $n$ de normale verdeling benadert. De stelling werd voor het eerst door De Moivre afgeleid in 1733 en later opgenomen in de tweede druk van The Doctrine of Chances van De Moivre, gepubliceerd in 1738. De stelling is genoemd naar Abraham de Moivre en Pierre-Simon Laplace. De stelling kan nu gezien worden als een speciaal geval van centrale limietstelling.

Stelling

Als de stochastische variabele $X_{n}$ binomiaal verdeeld is met parameters $n$ en $p$, geldt:

$\lim _{n\to \infty }P\left({\frac {X_{n}-np}{\sqrt {np(1-p)}}}\leq x\right)=\Phi (x),$

waarin $\Phi$ de verdelingsfunctie van de standaardnormale verdeling is.

Dit houdt in dat voor toenemende waarden van $n$ de verdeling van $X_{n}$ steeds dichter nadert tot een normale verdeling met verwachtingswaarde $np$ en variantie $np(1-p)$.

Bewijs

De stelling kan nu als een speciaal geval van de centrale limietstelling opgevat worden, maar moest door De Moivre apart als limiet bewezen worden. Daarbij maakte De Moivre gebruik van de door hem ontdekte vorm van de formule van Stirling, die een benadering met exponentiële functies geeft van een n! voor grote $n$.

Vuistregel

Als vuistregel hanteert men wel dat de benadering voldoende is voor waarden van $n$ en $p$, waarvoor zowel $np>5$ als $n(1-p)>5$.

Voorbeeld

Normale benadering van de binomiale verdeling met $n=48$ en $p=1/4$ door de normale verdeling met $\mu =12$ en $\sigma =3$

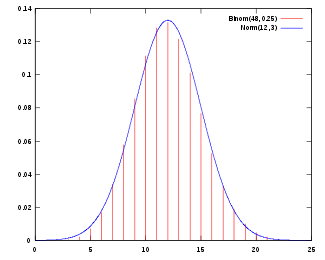
In de nevenstaande figuur zien we de binomiale verdeling met parameters $n=48$ en $p=1/4$ en de benaderende normale verdeling met $\mu =12$ en $\sigma =3$.