Driedeurenprobleem
Het driedeurenprobleem, soms naar het Engels Monty Hall-probleem genoemd, is een probleem uit de kansrekening en speltheorie dat vermoedelijk gebaseerd is op het eerder door Martin Gardner gepubliceerde probleem "De drie gevangenen". Het vraagstuk kan gezien worden als een paradox: er is geen logische tegenstrijdigheid, maar voor veel mensen gaat het resultaat in tegen hun intuïtie.
Achtergrond[bewerken | brontekst bewerken]
Het kreeg bekendheid door de Amerikaanse spelshow Let's Make a Deal met presentator Monty Hall; om die reden spreekt men in het Engels over het Monty Hall problem.
De formulering van het probleem, zoals het in september 1990 was gepubliceerd als ingezonden brief voor de rubriek Ask Marilyn van Marilyn vos Savant in het tijdschrift Parade luidt:
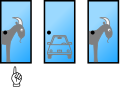
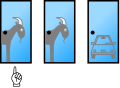
Stel dat je deelneemt aan een spelprogramma en je mag kiezen uit drie deuren: achter een van de deuren staat een auto, achter de andere twee staan geiten. Je kiest een deur, zeg nr. 1, en de presentator, die weet wat er achter de deuren staat, opent een andere deur, zeg nr. 3, met een geit erachter. Hij zegt dan tegen je: "Zou je deur nr. 2 willen kiezen?" Is het in je voordeel om van deur te wisselen?
— Whitaker 1990[1]
Vos Savant verduidelijkte dat de presentator in alle gevallen, dus zowel als de deelnemer de juiste deur kiest dan wel een verkeerde, een andere deur opent waarachter een geit staat en dat hij de deelnemer vervolgens altijd aanbiedt om van deur te wisselen. Belangrijk daarbij is dat de presentator weet achter welke deur de auto staat.
Door deze publicatie kreeg het probleem wereldwijd grote bekendheid. Eerder al, in 1975, was het probleem geformuleerd door Steve Selvin in een brief aan het tijdschrift The American Statistician van de American Statistical Association naar aanleiding van de spelshow Let's Make a Deal. In een volgende brief noemde Selvin het het Monty Hall problem.
Het driedeurenprobleem[bewerken | brontekst bewerken]

In een quiz wordt een deelnemer geconfronteerd met drie gesloten deuren. Achter een van de deuren staat een auto (of een ander waardevol voorwerp), achter de andere twee een geit (of iets anders van 'weinig' waarde). De deelnemer mag een deur aanwijzen en krijgt als prijs datgene wat zich achter die deur bevindt. Als de deelnemer een deur heeft aangewezen, opent de presentator een van de andere deuren waarachter een geit staat. De presentator geeft de deelnemer daarna de mogelijkheid om te wisselen van gesloten deur, dus om in plaats van de eerst gekozen deur te kiezen voor de andere nog gesloten deur. Wat moet de deelnemer doen? Kan hij beter wisselen van deur, of maakt het niets uit? Is de kans op het winnen van de auto groter als de deelnemer van deur wisselt?
Uit analyse blijkt dat het voor de deelnemer interessant is om van deur te wisselen, omdat de kans verandert van 1/3 naar 2/3. Velen vinden dit antwoord op het eerste gezicht tegenintuïtief en menen, omdat er nog twee mogelijkheden over zijn, dat de kansen 1/2 tegen 1/2 moeten zijn. Het is moeilijk in te zien dat er weliswaar twee mogelijkheden zijn, maar dat deze niet gelijke kansen hebben (omwille van de kennis van de presentator). Daarom volgt hieronder een analyse waarin verschillende scenario's onder de loep worden genomen.
Analyse[bewerken | brontekst bewerken]
Als de gebeurtenis als eenmalig voor de betrokken deelnemer wordt beschouwd is het onduidelijk of men nog over kansen moet spreken. De aanname is dat de quiz wordt herhaald. Dan kan worden nagegaan hoe vaak een bepaalde situatie zich voordoet, wat vertaald wordt in kansen.
Het is steeds een vraag naar een voorwaardelijke kans, wat inhoudt dat de kans berekend moet worden binnen de mogelijkheden die er zijn nadat de deelnemer een deur heeft aangewezen en de presentator een deur heeft geopend waarachter een geit blijkt te staan.
Uitgangssituatie[bewerken | brontekst bewerken]
Er wordt uitgegaan van de situatie dat de deelnemer deur 1 gekozen heeft en deur 3 geopend is en een geit laat zien. De mogelijkheden die zich gegeven de uitgangssituatie kunnen voordoen worden bekeken. Ook wordt ervan uitgegaan dat de auto geheel willekeurig achter een van de deuren is geplaatst en de deelnemer onbekend is met de plaats van de auto. Vergelijkbare uitgangssituaties waarin de deelnemer een andere deur gekozen heeft en de presentator een andere deur heeft geopend, geven, onder verwisseling van de deuren, aanleiding tot een vergelijkbare analyse.
Presentator[bewerken | brontekst bewerken]
De uiteindelijke oplossing is sterk afhankelijk van de strategie van de presentator. Er wordt verondersteld dat de presentator altijd een van de deuren met een geit erachter opent. Dus: als achter de deuren 2 en 3 allebei een geit staat, de presentator willekeurig een van deze twee deuren uitkiest.
Oplossing[bewerken | brontekst bewerken]
De manier waarop het probleem geformuleerd is wordt door velen beschouwd als het standaard 'driedeurenprobleem'. De oplossing hiervan wordt geformuleerd ervan uitgaande dat de speler aanvankelijk deur 1 aanwijst. Wanneer de speler de mogelijkheid wordt geboden van keuze te wisselen, is een nieuwe situatie ontstaan waarin deur 3 geopend is. Om een goede beslissing te nemen berekent de speler in deze nieuwe situatie de kans dat de auto achter deur 2 staat. Deze kans is een voorwaardelijke kans (Morgan et al. 1991; Gillman 1992; Grinstead and Snell 2006:137). Als de auto achter deur 2 staat, zal de presentator altijd deur 3 openen; deze situatie doet zich voor met kans 1/3. Als de auto achter deur 1 staat, zal de presentator maar in de helft van de gevallen deur 3 openen; deze situatie doet zich voor met kans 1/6. De auto staat in de gegeven situatie dus twee keer zo vaak achter deur 2 als achter deur 1. Door van keuze te wisselen wint de speler dus in 2/3 van de gevallen de auto.
Onderstaand is schematisch de gang van zaken weergegeven.
Er kan geconcludeerd worden dat iemand in dezelfde situatie als de deelnemer, dus waarin aanvankelijk deur 1 gekozen is en de presentator deur 3 opende (waarachter een geit zat), bij wisselen een (voorwaardelijke) kans op winst heeft van 2/3.
Een equivalente oplossing vergelijkt de kansen op de twee mogelijke situaties, namelijk: deur 1 gekozen, deur 3 geopend en de auto achter deur 1 met deur 1 gekozen, deur 3 geopend en de auto achter deur 2. Onder de gebruikelijke veronderstellingen is de kans op de tweede mogelijkheid 2 keer zo groot als op de eerste, omdat in het eerste geval de presentator nog de keuze had tussen het openen van deur 2 of deur 3, en hij in het tweede geval alleen deur 3 kon openen.
Formele oplossing[bewerken | brontekst bewerken]
De hierboven geschetste oplossing wordt formeel als volgt beschreven, ervan uitgaande dat de kandidaat deur 1 gekozen heeft. Een analoge analyse geldt voor andere keuzen van deur. De gebeurtenissen die zich kunnen voordoen zijn:
- ('Auto') met de betekenis: de auto staat achter respectievelijk deur 1, 2 of 3
- ('Quizmaster') met de betekenis: de presentator opent respectievelijk deur 1, 2 of 3,
en met kansen:
De voor de hand liggende strategie, waarin de kandidaat deur 1 had gekozen en de presentator vervolgens een deur met geit opent, waarbij hij als hij keuze heeft, willekeurig kiest, wordt bepaald door:
Als de kandidaat van keuze wisselt nadat deur 3 is geopend, wint hij de auto als deze achter deur 2 staat. De voorwaardelijke kans, gegeven dat deur 3 is geopend, op het winnen van de auto is volgens de formule van Bayes:
Oplossing met gebruik van symmetrie[bewerken | brontekst bewerken]
Met de keuze van deur 1 is de kans op de auto aanvankelijk 1/3. Door de strategie van de presentator wordt door het openen van deur 3 deze kans niet beïnvloed, want bewezen kan worden dat in de nieuwe situatie de (voorwaardelijke) kans op de auto ook 1/3 is. Bijgevolg is in de nieuwe situatie de (voorwaardelijke) kans op de auto achter deur 2 gelijk aan 2/3.
Bewezen moet worden dat door het openen van deur 3 de voorwaardelijke kans dat de auto achter deur 1 staat ook 1/3 is. Dit kan kort, op elegante wijze, door gebruik te maken van de aanwezige symmetrie.
De kans dat de auto achter deur 1 staat is 1/3. Dit is het (gewogen) gemiddelde van de voorwaardelijke kansen dat de auto achter deur 1 staat, voor elk van mogelijk geopende deuren door de presentator. Dat zou deur 2, of deur 3 kunnen zijn. Omdat verondersteld is dat de presentator met gelijke kansen een deur kiest om te openen als hij een keuze heeft, verandert er niets in het probleem als de deuren hernummerd worden. Daaruit volgt dat beide voorwaardelijke kansen aan elkaar gelijk zijn en dus gelijk aan de onvoorwaardelijke kans 1/3.
Vereenvoudigde uitleg[bewerken | brontekst bewerken]
Een eenvoudige redenering luidt als volgt. Als de quizkandidaat bij zijn keuze blijft, krijgt hij de auto als hij in het begin de deur met de auto had gekozen, en de kans daarop is 1/3. Wisselt hij van keuze, dan krijgt hij de auto als hij in het begin een deur met een geit had gekozen, en de kans daarop is 2/3. Deze kansen volgen uit het feit dat er willekeurig 2 geiten en 1 auto achter de drie deuren worden verstopt.
Discussie vereenvoudigde uitleg[bewerken | brontekst bewerken]
Volgens enkele bronnen (onder andere Morgan et al. 1991 en Gillman, Leonard (1992)) is deze redenering niet correct. De kandidaat krijgt de kans om te wisselen nadat hij een deur gekozen heeft (in de gegeven situatie is dit deur 1) en de quizmaster een deur met een geit (in de gegeven situatie deur 3) geopend heeft. Weliswaar is aanvankelijk de kans 1/3 op de auto achter deur 1, maar nadat de kandidaat een deur heeft gekozen en de quizmaster een deur heeft geopend zijn de oorspronkelijke kansen niet meer geldig. Dat ziet men direct aan de nieuwe kans op de auto achter deur 3. Deze nieuwe kans is 0, terwijl de oorspronkelijke kans 1/3 was. Het gaat er nu om de nieuwe kansen voor de deuren 1 en 2 te bepalen. Samen zijn ze 1, dus het is voldoende een van de twee te bepalen. Dan zal blijken dat de nieuwe kans voor deur 2 gelijk is aan 2/3, of alternatief dat de nieuwe kans voor deur 1 gelijk is aan 1/3, overigens dezelfde waarde als de oorspronkelijke kans. Men mag er echter niet zonder meer van uitgaan dat de nieuwe kans voor deur 1 dezelfde waarde heeft als de oude kans. Daarin ligt de door de bronnen gesignaleerde fout.
Waarom niet fifty-fifty?[bewerken | brontekst bewerken]
Veel mensen kunnen de oplossing nauwelijks geloven en menen dat na het openen van de deur met de geit, de overblijvende deuren gelijke kans hebben. Men dient echter te bedenken dat de deuren niet uitwisselbaar zijn. Ze onderscheiden zich doordat deur 1 aanvankelijk door de deelnemer is aangewezen en deur 2 door de presentator is dicht gelaten.
Het is anders voor iemand die na het openen van deur 3 de zaal binnenkomt en die van de voorgeschiedenis niet op de hoogte is (bij Vos Savant een groen mannetje uit een plotseling verschenen ruimteschip). Voor deze persoon is het wel om het even of hij wisselt van keuze of niet. Men moet daarbij natuurlijk wel bedenken dat bij herhaling, want daar gaat het om, zo'n persoon ook situaties tegenkomt waarin de deelnemer deur 2 heeft aangewezen.
Gemiddelde winstkansen[bewerken | brontekst bewerken]
Sommige auteurs beschouwen niet de bovenbesproken versie, waarin de deelnemer de keuze om te wisselen geboden wordt nadat hij een deur gekozen heeft en de presentator een deur met geit heeft geopend, maar de versie waarin ons, als publiek nog voordat de deelnemer zijn eerste keuze gemaakt heeft, gevraagd wordt of hij beter zal kunnen wisselen van deur. In deze situatie zijn de nummers van de aanvankelijk gekozen deur en de geopende deur niet bekend, en volstaat het te argumenteren dat, onder redelijke veronderstellingen, de kans op de auto achter de gekozen deur 1/3 is, en dus wisselen de auto met kans 2/3 geeft.
Andere auteurs vinden het moment waarop gevraagd wordt niet relevant voor het bepalen van de optimale strategie. Enerzijds is het duidelijk dat de strategie van "altijd wisselen" een winstkans garandeert van 2/3 (mits de auto initieel met kans 1/3 achter elke deur kan zijn). Deze overall winstkans is uiteraard de gemiddelde van de winstkansen behorend bij elke mogelijke situatie van de speler op het moment van zijn keuze. Stel nu dat de winstkans bij een van deze situaties kleiner dan 1/2 zou zijn. Dan zou men de winstkans in deze situatie, en daarmee ook de overall gemiddelde winstkans, kunnen verbeteren, door in deze specifieke situatie juist niet te wisselen. Maar het is eenvoudig in te zien dat ongeacht welke strategie men volgt, er altijd een deur aan te geven is, zodanig dat als de auto achter deze deur zou staan, men hem niet zal krijgen. En dit betekent, dat een gemiddeld winstkans van 2/3 niet te verbeteren is. En hieruit volgt dat de kans dat de auto achter de andere deur is, minstens 1/2 is, ongeacht de situatie. (We weten al dat het gemiddeld over alle mogelijke situaties, exact 2/3 is).
Voorbeeld: beschouw de strategie: "kies eerst deur 1. Als deur 2 wordt geopend, wissel niet. Als deur 3 wordt geopend, wissel wel". Bij deze strategie geldt dat men de auto niet zal krijgen als hij achter deur 3 staat. Men loopt dus minstens een kans van 1/3 om de auto niet te krijgen.
Samenvattend, hebben we de volgende twee feiten: (1) "Altijd wisselen" garandeert een succeskans, gemiddeld, van 2/3; (2) geen enkele strategie kan een betere gemiddelde succeskans geven. Het volgt hieruit dat de kans dat de auto achter de andere gesloten deur staat, gegeven het nummer van de eerst gekozen deur, en het nummer van de deur geopend door de spelleider, minstens gelijk is aan 1/2, voor elke mogelijke situatie. Dus wisselen is nooit onvoordelig. De strategie van "altijd wisselen" is eenvoudigweg niet te verbeteren.
We zien het driedeurenprobleem hier als een beslissingsprobleem. Wat is de slimste keuze voor de speler? Wat moet hij doen. Deze vraag kan volledig beantwoord worden zonder berekening van voorwaardelijke kansen. Sommige auteurs echter presenteren het driedeurenprobleem zuiver als een probleem in de kansrekening, en stellen dat de enige relevante kansen, de kansen zijn in de situatie waarop de keuze moet worden gemaakt.
De oorspronkelijke probleemstelling van Vos Savant laat zich dus op verschillende wijzen vertalen in een volledig gespecificeerd wiskundige probleem met eenduidige oplossing. De juiste oplossing hangt af van de achtergrond van de auteur en van het context waarin het probleem wordt gegeven, bijvoorbeeld: in een leerboek over kansrekening, of in een leerboek over beslissingstheorie?
Foutieve uitleg[bewerken | brontekst bewerken]
Een foutieve uitleg is dat de eerste keuze van de speler van deur 1 een kans van 1/3 op de auto inhoudt en wisselen, nadat de presentator deur 3 geopend heeft, dus de auto oplevert met kans 2/3. Equivalent met deze verkeerde uitleg is de redenering dat de auto met kans 1/3 achter de aanvankelijk gekozen deur 1 is, en de geopende deur 3 kans 0 op de auto heeft, zodat de resterende deur 2 een kans van 2/3 op de auto moet hebben. Of iets anders geredeneerd: dat de deuren 2 en 3 samen kans 2/3 op de auto hebben, en na het openen van deur 3 deze kans van 2/3 "overgaat" op deur 2. De beide laatste redeneringen zijn het gemakkelijkst te ontzenuwen, aangezien deur 2 en ook de geopende deur 3 elk een (aanvankelijke) kans 1/3 op de auto hebben. Dat na de keuze en het openen door de presentator deur 3 een nieuwe (voorwaardelijke) kans 0 op de auto heeft is duidelijk. Wat echter de nieuwe kansen voor de andere deuren zijn, moet eerst berekend worden, zowel voor deur 2 als voor deur 1. De fout in de eerste redenering schuilt daar in dat men klakkeloos veronderstelt dat de gekozen deur 1 die aanvankelijk een kans van 1/3 op de auto heeft, ook na het openen van deur 3 weer een (voorwaardelijke) kans 1/3 op de auto heeft. Dit is niet vanzelfsprekend en moet beargumenteerd worden.
Veronderstellingen[bewerken | brontekst bewerken]
Er zijn schrijvers die het niet eens zijn met de veronderstellingen dat de auto met gelijke kans 1/3 achter elke deur staat, en dat de presentator puur door toeval een deur opent als hij een keuze heeft. Hoewel dit niet expliciet in de probleemstelling staat vermeld, is het zeker vrij gebruikelijk bij elementaire problemen in de kansrekening te stellen dat keuze uit drie dingen de stilzwijgende veronderstelling inhoudt dat die keuze met gelijke kansen is. Hetzelfde geldt voor de presentator: aangezien niets vermeld wordt over een eventuele voorkeur, wordt stilzwijgend een keuze "at random" verondersteld. Dat is de reden dat sommige kansrekenaars deze veronderstellingen zonder verdere motivering maken. Deze ingrediënten zijn echter niet expliciet aanwezig in het door Marilyn vos Savant vermelde probleem, maar het probleem was dan ook niet formeel gesteld. Het probleem was gesteld door een niet-beroepswiskundige in een populair weekblad. Bovendien, een deel van zo'n puzzel is juist om goed gemotiveerde veronderstellingen te maken, waarmee een definitieve oplossing gevonden kan worden.
Vos Savant verweerde zich tegen de kritiek van sommige professionele kansrekenaars door te stellen dat zij met de door haar genoemde deurnummers "1" en "3" niet eens twee specifieke deuren bedoelde, maar voor het gemak de deur gekozen door de speler respectievelijk de deur geopend door de presentator achteraf zo benoemde (haar oorspronkelijke Engelse zin is ook volstrekt dubbelzinnig, en ongeacht haar feitelijke bedoeling, is elke uitleg goed te verdedigen). Vos Savant veronderstelt van tevoren (op grond van de symmetrieën van het probleem) dat de specifieke nummers irrelevant zijn. Haar vraag was bovendien niet een kansvraag, maar een strategievraag: zou je wisselen? Andere auteurs werpen tegen dat de speler wel degelijk weet welke van de drie deuren hij gekozen heeft en welke de presentator geopend heeft.
Hoe het ook zij, iedere schrijver is het erover eens dat je moet wisselen; waar onenigheid over bestaat is de vraag waarom. Volgens sommige auteurs moet men hiervoor een voorwaardelijke kans uitrekenen. Deze voorwaardelijke kans hangt echter af van de strategie van de presentator, en als die onbekend is aan de speler, kan de voorwaardelijke kans niet berekend worden, al kan men wel schatten dat die tussen 1/2 en 1 ligt. Dus is wisselen in ieder geval niet nadelig. Zoals gezegd is "altijd wisselen" juist optimaal, hetgeen aangetoond kan worden zonder de voorwaardelijke kansen uit te rekenen
Welke veronderstellingen men maakt over de verschillende kansen in het probleem, heeft verder veel te maken met de interpretatie van kansen die men prefereert. Voor sommige auteurs zijn kansen subjectief: ze kwantificeren de informatie die wij hebben over een bepaalde situatie. Voor zo'n subjectivist (ook wel een Bayesiaan genoemd, zie Bayesiaanse statistiek) geldt dat voor hem de kansen dat de spelleider deur 2 of deur 3 opent, in de situatie dat de speler deur 1 had gekozen, en de auto daar achter stond, juist aan elkaar gelijk zijn omdat hij geen enkele informatie hierover heeft. Voor de objectivist (ook wel frequentist genoemd) aan de andere kant, zijn deze kansen eigenschappen van de methodiek van de spelleider. Dit betekent:
- dat de kansen onbekend en willekeurig zijn
of
- dat extra informatie aan de probleemstelling toegevoegd moet worden zodat we eenduidige kansen kunnen uitrekenen.
Veel van de onenigheid tussen verschillende auteurs over hoe het probleem gesteld dient te worden, is af te leiden uit voorkeur van de auteurs voor een Bayesiaanse of een frequentistische interpretatie van kansen. Voor de subjectivist is de symmetrie van het probleem onder hernummering van de deuren zo vanzelfsprekend dat men van tevoren specifieke deurnummers weglaat. Het enige wat telt is de rol van elke deur en de relatie tussen de zichtbare en de verborgen rollen. Zichtbaar zijn: deur gekozen door de speler; deur geopend door de spelleider; deur die overblijft. Verborgen zijn: is er een auto achter de eerst gekozen deur, of achter de deur die dichtblijft?
Vanuit deze optiek negeert men de specifieke deurnummers, ongeacht het feit dat ze wel aan de speler bekend zijn. De eenvoudige oplossing is correct zonder het noemen van "deurnummers: de auto is achter de eerst gekozen deur met kans 1/3, is niet achter de deur die door de spelleider is geopend, en is dus achter de overgebleven gesloten deur met kans 2/3.
Alternatieven[bewerken | brontekst bewerken]
De probleemstelling, zoals die is afgeleid uit wat zich bij de quiz afspeelde, laat ruimte voor andere interpretaties. In de wetenschappelijke literatuur zijn alternatieve mogelijkheden bestudeerd (zie onder andere Granberg, 1996; Granberg & Brown, 1995; Morgan, 1991; Gill, 2010). Enkele van deze alternatieve interpretaties staan hieronder.
Standaard uitgangssituatie[bewerken | brontekst bewerken]
Bij de eerste gevallen is de situatie als bij het standaardprobleem, dus deur 1 door de deelnemer gekozen en de presentator heeft deur 3 geopend en er staat een geit achter, maar beschouwen we andere strategieën van de presentator volgt een ander strategie.
- Geval 1
De deelnemer heeft aanvankelijk deur 1 gekozen en de presentator opent willekeurig een van de andere deuren, eventueel de auto tonend. Deze spelvariant heeft twee subvarianten: de deelnemer mag slechts kiezen uit de twee nog niet geopende deuren, dus als de auto achter de geopende deur staat krijgt hij deze niet, of hij krijgt hem dan juist wel. Nu de presentator een deur met een geit heeft geopend is dit niet meer van belang.
Er zijn zes even waarschijnlijke mogelijkheden:
auto achter deur 1 1 2 2 3 3 mogelijk te openen deur 2 3 2 3 2 3 presentator opent deur 3 * * winst bij wisselen x
Een van de twee mogelijkheden met een * heeft zich voorgedaan: deur 3 is immers open en toont een geit. Winst bij wisselen is hier dus bij de mogelijkheid x, een van twee even waarschijnlijke. De voorwaardelijke kans op winst bij wisselen is dus 1/2.
De overall winstkans bij de eerste subvariant van het spel is 1/3 (de kans was 2/3 dat achter de geopende deur een geit zou staan, vervolgens was de winstkans 1/2) en bij de tweede 2/3 (de kans dat achter de geopende deur de auto zou staan was 1/3, dit is de extra winstkans in deze subvariant van het spel).
- Geval 2
De presentator opent deur 3 als daar een geit achter staat, en anders deur 2. Er zijn drie even waarschijnlijke mogelijkheden:
auto achter deur 1 2 3 te openen deur 3 3 2 presentator opent deur 3 * * winst bij wisselen x
Daarvan heeft een van de twee met een * zich voorgedaan. Winst bij wisselen is hier dus bij de mogelijkheid x, een van twee even waarschijnlijke. De voorwaardelijke kans op winst bij wisselen is dus 1/2.
- Geval 3
De presentator opent als het kan, dat wil zeggen als er een geit achter staat, deur 2, en anders deur 3. Er zijn 3 even waarschijnlijke mogelijkheden:
auto achter deur 1 2 3 te openen deur 2 3 2 presentator opent deur 3 * winst bij wisselen x
Daarvan heeft * zich voorgedaan. Winst bij wisselen is hier dus bij de mogelijkheid x en levert met zekerheid de auto.
Andere uitgangssituatie[bewerken | brontekst bewerken]
Het is bij de uitgangssituatie van belang dat men weet welke deur geopend is. In sommige "verklaringen" van het probleem houdt men daar (al dan niet bewust) geen rekening mee. Zo'n situatie kan eventueel als volgt beschreven worden. Nadat de deelnemer een deur (zeg deur 1) heeft aangewezen, legt de presentator uit dat hij van plan is een van de andere twee deuren te openen. Voordat hij dat daadwerkelijk uitvoert, vraagt hij de deelnemer nu al te beslissen of deze straks, als de deur geopend is en er een geit achter staat, wil wisselen van keuze
- Geval 4
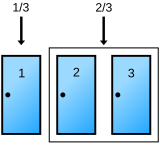
De presentator opent altijd een van de deuren met een geit erachter. Omdat er altijd een geit achter een van de andere deuren staat, worden bij deze strategie de mogelijkheden niet beperkt. (In de figuur zou eigenlijk een van de deuren geopend moeten zijn, alleen weten we niet welke.) De mogelijkheden zijn immers:
auto achter deur 1 1 2 3 te openen deur 2 3 3 2 mogelijkheden * * * * winst bij wisselen x x
Al deze vier mogelijkheden kunnen voorkomen in de uitgangssituatie. De gevraagde voorwaardelijke kans is dus gelijk aan de onvoorwaardelijke. Omdat de deelnemer met kans 1/3 de auto wint als hij bij zijn keuze blijft, verhoogt hij z'n kans tot 2/3 door te wisselen en de andere, niet-geopende deur te kiezen. Merk op dat de beide mogelijkheden dat de auto achter deur 1 staat samen kans 1/3 hebben.
- Geval 5
De presentator opent willekeurig een van de andere deuren, eventueel de auto tonend. Er zijn zes even waarschijnlijke mogelijkheden:
auto achter deur 1 1 2 2 3 3 mogelijk te openen deur 2 3 2 3 2 3 mogelijkheden * * * * winst bij wisselen x x
waarvan een van de vier met een *, waarbij achter de geopende deur een geit staat, zich heeft voorgedaan. De voorwaardelijke kans op winst bij wisselen is dus de kans om binnen de mogelijkheden met een * de auto te winnen. Dat gebeurt bij de mogelijkheden met een x, dus bij 2 van de 4 even waarschijnlijke mogelijkheden, dus met kans 1/2.
- Geval 6
De presentator opent alleen een deur (met een geit) als de auto achter deur 1 (de keuze van de deelnemer) staat. Omdat hij in het beschouwde geval een deur met een geit heeft geopend, weet de deelnemer dat achter de andere deur ook een geit staat. Hij blijft bij z'n keuze en wint de auto.
- Geval 7
De presentator opent deur 3 als er een geit achter staat, anders deur 2. Er zijn 3 even waarschijnlijke mogelijkheden.
auto achter deur 1 2 3 te openen deur 3 3 2 presentator opent deur 3 * * winst bij wisselen x
waarvan een van de twee met een * zich heeft voorgedaan. Winst bij wisselen is hier dus bij mogelijkheid x, een van twee even waarschijnlijke, dus de voorwaardelijke kans is 1/2.
- Geval 8
De presentator opent deur 2 als er een geit achter staat, anders deur 3. Dit geval is equivalent met geval 7.
Uitbreiding naar meer deuren[bewerken | brontekst bewerken]
Een eenvoudige manier om in te zien dat de kans om de auto te winnen groter wordt door te wisselen van deur, bestaat uit het uitbreiden van het probleem naar meer deuren. Als voorbeeld kan men 10 in plaats van 3 deuren nemen. Daarbij blijft er nog altijd één auto, en zijn er dus negen geiten. Nadat de deelnemer een willekeurige deur genomen heeft, opent de presentator acht andere deuren waarbij er alleen geiten verschijnen. Er blijven dan nog twee gesloten deuren over: de deur die de deelnemer gekozen heeft, zeg voor het gemak deur 1, en een andere deur, bijvoorbeeld deur 2. De deuren 3 tot en met 10 staan open en laten een geit zien.
Aangezien er tien deuren zijn, zijn er tien mogelijkheden voor de deelnemer om een deur te kiezen. Daarbij is hij slechts in 1 van die mogelijkheden winnaar, in de 9 andere gevallen verliest hij.
Bij de eerste mogelijkheid - de deelnemer kiest de juiste deur - verliest de deelnemer als hij van deur verandert. De kans hierop is vooraf bekeken 1/10. Als het openen van de andere deuren door de presentator de kans niet veranderd heeft, is ook na het openen van de 8 deuren deze kans nog steeds 1/10.
Bij de negen andere mogelijkheden, waarbij de deelnemer de verkeerde deur kiest, opent de presentator alle andere deuren, behalve diegene waarachter zich de auto bevindt. In die negen gevallen is het dus aangewezen voor de deelnemer om van deur te veranderen, omdat die keuze altijd de auto oplevert. Dus in negen van de tien gevallen doet de deelnemer er goed aan van deur te wisselen. Maar de vraag is of hij er goed aan doet van deur te wisselen in de gegeven situatie, waarin hij als eerste keuze deur 1 heeft gekozen en de deuren 3 tot en met 8 open staan.
Als bewezen kan worden dat ook in deze situatie de kans op de auto achter deur 1 ook 1/10, neemt de kans op de auto toe van 1/10 naar 9/10 indien de deelnemer van deur wisselt. Dit uiteraard enkel in het geval dat de presentator weet achter welke deur de auto staat. Maar dit is impliciet vervat in de probleemstelling, aangezien de mogelijkheid dat de presentator een deur opent waarachter zich de auto bevindt, niet voorkomt.
Er blijft dus slechts over te bewijzen dat in de gegeven situatie de kans op de auto achter deur 1 ook 1/10 is.
Dit probleem terug reduceren naar drie deuren geeft dat wisselen van deur de kans om te winnen van 1/3 naar 2/3 brengt.
Formeel bewijs voor deuren[bewerken | brontekst bewerken]
Terwijl het eenvoudig is in te zien dat de bewering dat veranderen de juiste strategie is indien een groter aantal deuren beschouwd wordt, kan men ook formeel aantonen dat dit zo is.
Dit kan met een veralgemening naar deuren (met een natuurlijk getal groter of gelijk dan 3) en door gebruik te maken van voorwaardelijke kansberekening. Daarbij gelden de volgende definities voor gebeurtenissen:
- ('auto') met de betekenis: de auto staat achter deur (met )
- : de kandidaat kiest deur (met )
- ('closed') met de betekenis: de presentator opent alle deuren behalve deur en deur (met )
Verondersteld wordt dat en voor elke en onderling onafhankelijk zijn.
Vanwege de willekeurige plaatsing van de auto en de bovengenoemde onafhankelijkheid is voor elke :
Uitgaande van de veronderstellingen:
- de kandidaat kiest voor deur met ,
- de presentator opent alle andere deuren, behalve de door de kandidaat gekozen deur en één andere deur, waarbij alleen geiten tevoorschijn komen,
kan men de volgende kansen berekenen:
- voor . Met andere woorden, als de kandidaat de juiste deur gekozen heeft, kan de presentator nog deuren openen, waarvan hij er 1 dicht laat. Daarbij maakt het niet uit welke deur hij dicht laat, aangezien er overal een geit achter staat. In dat geval is de kans dat hij een bepaalde deur dicht laat dus .
- voor . Immers, als de kandidaat deur kiest waar een geit achter staat, zal de presentator die deur en de deur met de auto dichtlaten.
- voor de gevallen met zowel als . Immers, als de kandidaat deur kiest en de auto staat achter deur , dan opent de presentator alle andere deuren met uitzondering van de deur met de auto.
De kans om de auto te winnen bij wisselen van deur kan, gebruik makend van de formule van Bayes, als volgt worden berekend:
Voor iedere geldt:
- .
Bij geeft deze formule inderdaad , en bij geeft dit . Ook is hiermee duidelijk dat wisselen voor een willekeurige , groter of gelijk aan 3, een kans geeft van meer dan 50%, en dus dat het altijd de aangewezen strategie is.
Opmerking[bewerken | brontekst bewerken]
Er zijn verschillende opvattingen over wat eigenlijk met kans bedoeld is. Als de kandidaat aanvankelijk een van de drie deuren mag kiezen, bedoelen velen (maar niet iedereen: zie Bayesiaanse kans) met te zeggen dat de kans 1/3 is dat de auto achter de gekozen deur staat het volgende: in de verschillende uitzendingen van de quiz zal een van de drie keer achter deze deur de auto staan. Welke keren dat zijn weet men vooraf niet.
Als de kandidaat een deur heeft aangewezen en de presentator opent een deur met een geit, hoe liggen de (voorwaardelijke) kansen dan? Dat de (voorwaardelijke) kans 1/3 is dat de auto achter de aangewezen deur staat, betekent het volgende: van alle keren dat een kandidaat een bepaalde deur heeft aangewezen en de presentator - met de juiste strategie - een deur met een geit heeft geopend, staat een op de drie keer de auto inderdaad achter de oorspronkelijk door de kandidaat aangewezen deur. In de volgende tabel staan voor het geval dat de kandidaat deur 1 heeft aangewezen, alle mogelijkheden (die vallen binnen de door de presentator gevolgde strategie), met de kans van optreden.
Bekijk nu de twee met * aangeduide situaties: de kandidaat heeft deur 1 aangewezen en de presentator heeft deur 3 waar een geit achter staat geopend.
auto achter deur 1 1 2 3 kans 1/3 1/3 1/3 presentator opent 2 3 3 2 kans per deur 1/2 1/2 1 1 kans op auto 1/6 1/6 1/3 1/3 deur 3 is geopend * * voorw. kans 1/3 2/3
Van de twee gevallen met * is de (voorwaardelijke) kans dat de auto achter deur 2 staat twee keer zo groot (1/3) als de kans dat hij achter deur 1 staat (1/6).
In de bovenstaande uitleg wordt ervan uitgegaan dat de presentator altijd een alternatieve deur aanbiedt, welke deur de kandidaat ook gekozen heeft. Als de presentator alleen de mogelijkheid aanbiedt een andere deur te kiezen als achter de eerstgekozen deur de auto staat, dan komt het erop neer dat de presentator aan het proberen is de kandidaat van een correcte keuze af te brengen, en kan de kandidaat dus beter niet zijn keuze wijzigen. Als het spel vaker gespeeld wordt, steeds op deze manier, dan zal dit ook blijken. Bij een eenmalig spel kan de kandidaat door naar de presentator te kijken proberen vast te stellen of die hem voor de gek houdt of helpt.
Ongeloof[bewerken | brontekst bewerken]
Het probleem was zo intrigerend dat Marilyn vos Savant deze Monty Hall-deal opnieuw in haar column van 9 september 1990 aan de orde stelde, met de opmerking dat de winstkans tweemaal zo groot werd als men van deur zou verwisselen. Dit ontlokte een storm van protest, waarbij zelfs de beroemde en productiefste wiskundige aller tijden Paul Erdős, na – via een bovenstaande analyse, in Ask Marilyn – het bewijs van dubbele winstkans na wisselen van deur vernomen te hebben, stellig verklaarde dat "het geen verschil zou moeten maken". Na uitleg met behulp van een beslissingsboom raakte hij zelfs nog geïrriteerder, en pas na een simulatie gaf hij toe dat hij fout zat.
Bridge[bewerken | brontekst bewerken]
Bij het spelen van het kaartspel bridge komen geregeld soortgelijke keuzes aan de orde. In de bridgeliteratuur wordt deze groep problemen aangeduid met de naam restricted choice.
Literatuur[bewerken | brontekst bewerken]
- Adams, Cecil (1990). "On 'Let's Make a Deal,' you pick Door #1. Monty opens Door #2—no prize. Do you stay with Door #1 or switch to #3?", The Straight Dope (2 november 1990). Geraadpleegd op 25 juli 2005.
- Bapeswara Rao, V. V. and Rao, M. Bhaskara (1992). "A three-door game show and some of its variants". The Mathematical Scientist 17(2): 89–94.
- Behrends, Ehrhard (2008). Five-Minute Mathematics. AMS Bookstore, p. 57. ISBN 9780821843482.
- Bloch, Andy, 21 - The Movie (my review) (2008). Gearchiveerd op 7 mei 2008. Geraadpleegd op 5 mei 2008.
- Chun, Young H. (1991). "Game Show Problem", OR/MS Today 18(3): 9.
- Devlin, Keith, Devlin's Angle: Monty Hall. The Mathematical Association of America (juli – augustus 2003). Gearchiveerd op 13 april 2008. Geraadpleegd op 25 april 2008.
- Fox, Craig R. and Levav, Jonathan (2004). "Partition-Edit-Count: Naive Extensional Reasoning in Judgment of Conditional Probability", Journal of Experimental Psychology: General 133(4): 626-642.
- Gardner, Martin (1959a). Column "Mathematical Games", Scientific American, October 1959, p. 180–182. Reprinted in The Second Scientific American Book of Mathematical Puzzles and Diversions.
- Gardner, Martin (1959b). Column "Mathematical Games", Scientific American, november 1959, p. 188.
- Gill, Richard (2010). Monty Hall problem. pp. 858–863, International Encyclopaedia of Statistical Science, Springer, 2010.
- Gillman, Leonard (1992). "The Car and the Goats", American Mathematical Monthly 99: 3–7.
- Gnedin, Sasha, "The Mondee Gills Game"[dode link]. The Mathematical Intelligencer, 2011.
- Granberg, Donald (1996). "To Switch or Not to Switch". Appendix to vos Savant, Marilyn, The Power of Logical Thinking. St. Martin's Press. ISBN 978-0-312-13985-8.
- Granberg, Donald and Brown, Thad A. (1995). "The Monty Hall Dilemma", Personality and Social Psychology Bulletin 21(7): 711-729.
- Grinstead, Charles M. and Snell, J. Laurie (4 juli 2006). Grinstead and Snell’s Introduction to Probability (PDF), Online versie van Introduction to Probability, 2nd edition, published by the American Mathematical Society, Copyright (C) 2003 Charles M. Grinstead and J. Laurie Snell.. Geraadpleegd op 2 april 2008.
- Hall, Monty (1975). The Monty Hall Problem. LetsMakeADeal.com. Bevat de brief aan Steve Selvin van 12 mei 1975. Geraadpleegd op 15 januari 2007.
- Krauss, Stefan and Wang, X. T. (2003). "The Psychology of the Monty Hall Problem: Discovering Psychological Mechanisms for Solving a Tenacious Brain Teaser", Journal of Experimental Psychology: General 132(1). Gevonden op MontyHallPaper.pdf, 30 maart 2008.
- Mack, Donald R. (1992). The Unofficial IEEE Brainbuster Gamebook. Wiley-IEEE, p. 76. ISBN 9780780304239.
- Magliozzi, Tom; Magliozzi, Ray (1998). Haircut in Horse Town: & Other Great Car Talk Puzzlers. Diane Pub Co.. ISBN 0-7567-6423-8.
- Martin, Robert M. (2002). There are two errors in the the title of this book, 2nd. Broadview Press, 57–59. ISBN 9781551114934.
- Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). "Let's make a deal: The player's dilemma", American Statistician 45: 284-287.
- Rosenthal, Jeffrey S., Monty Hall, Monty Fall, Monty Crawl 5–7 (september 2008).
- Selvin, Steve (1975a). "A problem in probability" (letter to the editor). American Statistician 29(1): 67 (February 1975).
- Selvin, Steve (1975b). "On the Monty Hall problem" (letter to the editor). American Statistician 29(3): 134 (August 1975).
- Seymann R. G. (1991). "Comment on Let's make a deal: The player's dilemma", American Statistician 45: 287-288.
- vos Savant, Marilyn (1990). Column "Ask Marilyn", Parade Magazine p. 16 (9 september 1990).
- vos Savant, Marilyn (1996). The Power of Logical Thinking. St. Martin's Press. ISBN 0-312-13985-3.
- vos Savant, Marilyn (2006). Column "Ask Marilyn", Parade Magazine p. 6 (26 november 2006).
- Whitaker, Craig F. (1990). [Letter]. Column "Ask Marilyn", Parade Magazine p. 16 (9 september 1990).
Externe links[bewerken | brontekst bewerken]
Bronnen, noten en/of referenties
|