Wet van Zipf

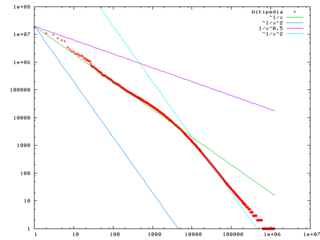
De wet van Zipf is oorspronkelijk de door George Kingsley Zipf (1902-1950)[1] geconstateerde en naar hem genoemde wetmatigheid in de taalkunde, dat in natuurlijke taal de frequentie van voorkomen van een woord ruwweg omgekeerd evenredig is met de rang van het woord in de frequentietabel, en wel zo dat het meest frequente woord ongeveer twee keer zo vaak voorkomt als het op een na frequentste woord, drie keer zo vaak als het op twee na frequentste enz. Met de Wet van Zipf worden tegenwoordig kansverdelingen aangeduid die de vorm van een machtswet hebben. De wet kan gekarakteriseerd worden door het lineaire verband tussen de logaritmen van rangnummer en kans of frequentie. In dubbellogaritmische weergave is het verband een rechte lijn.
De constatering door Zipf markeert het begin van de kwantitatieve linguïstiek. Buiten de linguïstiek duikt dit verband evenwel ook in uiteenlopende andere domeinen op. Zo blijkt het verband tussen de rang en de bevolking van de grootste steden in de Verenigde Staten en verschillende andere landen overeen te komen met de wet van Zipf. De "wetenschappelijke productiviteit" (aantal publicaties of referenties naar publicaties van wetenschappers) en het aantal maal per maand dat de webpagina's van een website worden bezocht zijn andere voorbeelden van data die de wet van Zipf volgen.[2] Alfred Lotka (1880-1949) vond dat de vorm van deze verdeling weinig of niets zegt over de onderliggende, fysische verbanden:
"Frequency distributions of this general type have a wide range of applicability to a variety of phenomena, and the mere form of such a distribution throws little or no light on the underlying physical relations."
Definitie[bewerken | brontekst bewerken]
Onder een verdeling volgens de wet van Zipf, of kort een Zipf-verdeling, verstaat men een discrete kansverdeling met parameters en , voor gedefinieerd door
Ze is later gebruikt voor onder meer de wet van Bradford (sociale wetenschappen) en het Paretoprincipe (economie).[bron?]
Zie ook[bewerken | brontekst bewerken]
- Machtswet
- Pareto-verdeling
- Complexe netwerken
- Dikke staart (long tail)
- Fractal
- Centrale-plaatsentheorie
|
Bron
Voetnoten
|




