Asymptoot
In de wiskunde is een asymptoot van een functie of de grafiek ervan een rechte lijn of een kromme waar de grafiek van die functie willekeurig dicht toe nadert als het argument naar een limiet nadert (eventueel plus of min oneindig). De term is afgeleid uit het Grieks en betekent letterlijk niet samenvallen (overigens sluit de genoemde definitie samenvallen niet uit). Asymptoten worden vaak gebruikt als hulpmiddel bij het tekenen van grafieken. Een deelgebied van de wiskunde, de asymptotiek, bestudeert het gedrag van functies in de buurt van of bij een punt waar de functie onbegrensd is.
Rechte lijnen als asymptoten[bewerken | brontekst bewerken]

in het rood, asymptoten blauw en groen
De belangrijkste asymptoten zijn rechte lijnen; daarin onderscheidt men drie gevallen:
- Verticale asymptoot:
- Horizontale asymptoot:
- Schuine of scheve asymptoot:
Merk op dat de horizontale asymptoot in deze definitie een bijzonder geval is van de schuine asymptoot, waarbij .
Verticale asymptoot[bewerken | brontekst bewerken]
Verticale asymptoten komen voor indien de kromme aan minstens een van beide kanten rond het punt naar oneindig gaat. Als men zich beperkt tot asymptoten aan functies, dan kan deze voorwaarde als volgt geformuleerd worden: de rechte is een verticale asymptoot van , indien voldaan is aan:
of
Horizontale asymptoot[bewerken | brontekst bewerken]

in het rood, asymptoten blauw en groen
Er is sprake van een horizontale asymptoot als de kromme voor steeds grotere en/of kleinere x-waarden, ongeveer evenwijdig gaat lopen aan de x-as. Als dit het geval is op een hoogte , dan is dit de vergelijking van de asymptoot. Opnieuw kan dit met limieten formeler genoteerd worden:
of
In het eerste geval is er een horizontale asymptoot langs de positieve -as, in het tweede geval is deze langs de negatieve x-as. Indien beide limieten bestaan, heeft de functie twee asymptoten die samenvallen in het geval dat .
Schuine asymptoot[bewerken | brontekst bewerken]
De schuine asymptoot is een rechte lijn met algemene vergelijking . Formeel is deze rechte een asymptoot van indien:
of
Voor de parameters en geldt:
en

in het rood, asymptoten blauw en groen
Voorbeelden[bewerken | brontekst bewerken]
- Figuur 1:
- Er is een verticale asymptoot , de -as (groen): daar wordt de noemer 0 en gaat naar negatief oneindig langs links en naar positief oneindig langs rechts. Voor gaande naar (oneindig) gaat naar 0, dus de -as (blauw) met als vergelijking is een horizontale asymptoot. De grafiek is een orthogonale hyperbool.
- Figuur 2:
- De tangensfunctie heeft verticale asymptoten bij , immers, deze functie gaat daar naar oneindig. Omgekeerd zal de inverse functie daardoor horizontale asymptoten bezitten voor , deze zijn respectievelijk in het groen en blauw weergegeven.
- Figuur 3:
- Om dezelfde reden als in figuur 1, vinden we de -as als verticale asymptoot terug. Daarnaast vinden we nu ook:
- zodat we een schuine asymptoot vinden met vergelijking . In dit geval kon men dit reeds aan zien, daar de term naar 0 zal gaan voor gaande naar waardoor overblijft.
- De grafiek is een hyperbool, en dus symmetrisch in de lijn door de oorsprong met een helling van 67,5 graden.
Toepassing: rationale functies[bewerken | brontekst bewerken]
Indien de functie een rationale functie (een breuk van veeltermen) is, kunnen de asymptoten systematisch gevonden worden. Beschouwen we twee veeltermen en , zonder gemeenschappelijke nulpunten. We kunnen de staartdeling uitvoeren zodat we een veelterm verkrijgen en een rest waarvan de graad kleiner is dan die van . We schrijven dus:
Men kan dan de volgende conclusies trekken in verband met de aanwezigheid van asymptoten:
- Elk nulpunt van levert een verticale asymptoot in dat punt
- Indien een constante waarde heeft, dan is er een horizontale asymptoot
- Indien de graad van gelijk is aan 1, dan is een schuine asymptoot.
Willekeurige kromme als asymptoot[bewerken | brontekst bewerken]

in het rood, asymptoten blauw en groen
Zoals beschreven in de inleiding, hoeven asymptoten niet noodzakelijk rechten te zijn. Een willekeurige kromme kan in het algemeen ook asymptoten hebben die zelf niet lineair zijn. Zo is een asymptotische kromme van
We illustreren dit met een ander voorbeeld, beschouw de functie:
Door de vierkantswortel en de noemer is enkel gedefinieerd voor positieve getallen. Aangezien:
zal voor het gedrag van voor grote waarden van quasi volledig bepaald zijn door de vierkantswortel.
Men kan dan ook als een asymptotische curve zien van , in figuur 4 aangeduid in het blauw.
Bovendien heeft door de aanwezigheid van de term ook weer de -as als verticale asymptoot, aangeduid in het groen.
Opmerkingen[bewerken | brontekst bewerken]
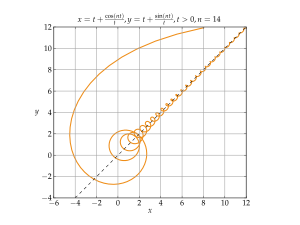
- Een kromme kan meerdere verticale asymptoten hebben. Als we functies beschouwen, zijn deze daar niet continu.
- Men kan op oneindig geen verschillende asymptoten hebben. Omdat er zowel op positief als op negatief oneindig een asymptoot kan voorkomen, is het aantal van dit type asymptoten beperkt tot twee. Het is dus bijvoorbeeld mogelijk dat een kromme zowel een horizontale als een schuine asymptoot heeft, al moeten deze dan wel aan verschillende kanten van de y-as liggen.
- Aan de hand van de gegeven voorbeelden zou men kunnen denken dat een kromme zijn asymptoot nooit snijdt, maar op oneindig raakt. Hoewel dit vaak het geval is, zeker voor functies, hoeft dit niet zo te zijn. In figuur 5 is een kromme weergegeven die zijn asymptoot oneindig vaak snijdt, maar deze wel (in overeenstemming met de definitie) willekeurig dicht nadert.
- Men onderscheidt in de wiskunde nog andere betekenissen van asymptotisch gedrag; dit is afhankelijk van de context. In verschillende gevallen heten en asymptotische krommen voor gaande naar oneindig als:
- naar 0 gaat.
- naar 1 gaat.
- een eindige limiet heeft, verschillend van 0.
- begrensd is, maar niet naar 0 gaat.





















































