Tangens en cotangens

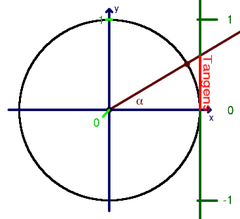
Tangens en cotangens zijn goniometrische functies. De naam tangens komt van raaklijn in het Latijn (tangens betekent rakend). Het argument van de tangens en de cotangens wordt vaak gezien als een hoek en dat heeft te maken met de oorspronkelijke definitie van deze functies. De tangens was gedefinieerd als de verhouding van de overstaande en de aanliggende rechthoekszijde in een rechthoekige driehoek. Deze oorspronkelijke definitie beperkte echter het domein van het argument van 0° tot 90° (behalve 90° zelf, waarvoor de tangens niet gedefinieerd is).

De inverse functie van de tangens is de arctangens of boogtangens, die voor een gegeven waarde van de tangens als functiewaarde de oorspronkelijke hoek (tussen −90° en +90°) geeft.

Goniometrische cirkel (eenheidscirkel)

• 

  tangens van $\alpha$ in de eenheidscirkel

• 

  cotangens van $\alpha$

De functiewaarde van de tangens loopt van $0$ tot $\infty$ voor een argument lopend van 0° tot 90°, en van $-\infty$ terug naar $0$ voor een argument lopend van 90° tot 180°. Daarbuiten wordt de functie periodiek (periode = 180°) voortgezet. Ook geldt:

$\tan(-\alpha )=-\tan \alpha$

Beide functies kunnen uitgedrukt worden in de sinus en de cosinus:

$\tan \alpha ={\frac {\sin \alpha }{\cos \alpha }}$

$\cot \alpha ={\frac {\cos \alpha }{\sin \alpha }}$

De cotangens van een hoek is dus de omgekeerde van de tangens van die hoek (mits $\cos \alpha \neq 0$ en $\sin \alpha \neq 0$):

$\cot \alpha ={\frac {1}{\tan \alpha }}$

De tangens wordt dus aangeduid met $\tan$ en de cotangens met $\cot$. Ook komen de verouderde afkortingen $\mathrm {tg}$ en $\mathrm {cotg}$ nog wel voor.

Bijzondere waarden

graden	0°	30°	45°	60°	90°	120°	135°	150°	180°	270°
radialen	$0\,$	${\tfrac {1}{6}}\pi$	${\tfrac {1}{4}}\pi$	${\tfrac {1}{3}}\pi$	${\tfrac {1}{2}}\pi$	${\tfrac {2}{3}}\pi$	${\tfrac {3}{4}}\pi$	${\tfrac {5}{6}}\pi$	$\pi \,$	${\tfrac {3}{2}}\pi$
tangens	$0\,$	${\tfrac {1}{3}}{\sqrt {3}}$	$1\,$	${\sqrt {3}}$	geen	$-{\sqrt {3}}$	$-1\,$	$-{\tfrac {1}{3}}{\sqrt {3}}$	$0\,$	geen
cotangens	geen	${\sqrt {3}}$	$1\,$	${\tfrac {1}{3}}{\sqrt {3}}$	$0\,$	$-{\tfrac {1}{3}}{\sqrt {3}}$	$-1\,$	$-{\sqrt {3}}$	geen	$0\,$

Machtreeks

De tangens en cotangens kunnen ook in de vorm van een machtreeks geschreven worden, bijvoorbeeld als Taylorreeks. Voor $|x|<{\tfrac {\pi }{2}}$ geldt:

$\tan x=x+{\tfrac {1}{3}}x^{3}+{\tfrac {2}{15}}x^{5}+{\tfrac {17}{315}}x^{7}+\ldots =\sum _{n=1}^{\infty }|B_{2n}|{\frac {2^{2n}\left(2^{2n}-1\right)}{(2n)!}}x^{2n-1}$

$\cot x=x^{-1}-{\tfrac {1}{3}}x-{\tfrac {1}{45}}x^{3}-{\tfrac {2}{945}}x^{5}-\ldots =\sum _{n=0}^{\infty }(-1)^{n}B_{2n}{\frac {2^{2n}}{(2n)!}}x^{2n-1}$

Daarin is $B_{n}$ het zogenaamde $n$-de Bernoulligetal.

Beschouwt men $x$ als hoek, dan is $x$ uitgedrukt in radialen.

Praktische toepassingen

Schaduwlengte

De lengte $L$ van de slagschaduw van een voorwerp kan geschreven worden als functie van de zonnehoek $\alpha$ en de loodrechte hoogte $H$ van het voorwerp:

$L={\frac {H}{\tan \alpha }}$

Driehoeksmeetkunde

In een driehoek $ABC$ geldt voor de grootte van de hoeken:

$\tan A+\tan B+\tan C=\tan A\cdot \tan B\cdot \tan C$

$\cot {\frac {A}{2}}+\cot {\frac {B}{2}}+\cot {\frac {C}{2}}=\cot {\frac {A}{2}}\cdot \cot {\frac {B}{2}}\cdot \cot {\frac {C}{2}}$

Zie ook

• Tangensregel
• Sinus en cosinus
• Goniometrische functie
• Arctangens
• Arccotangens

Externe links

• microcursus goniometrie voor beginners
• Tabellenboek goniometrie

Wiskundige functies
Basisfuncties: optellen · aftrekken · vermenigvuldigen · delen · machtsverheffen · worteltrekken Logaritme: logaritme · natuurlijke logaritme · exponentiële functie Trigonometrie: sinus en cosinus · tangens en cotangens · secans en cosecans Inverse functies: arcsinus · arccosinus · arctangens · arccotangens · arcsecans · arccosecans Overig: hyperbolische functies