Cyclometrische functie

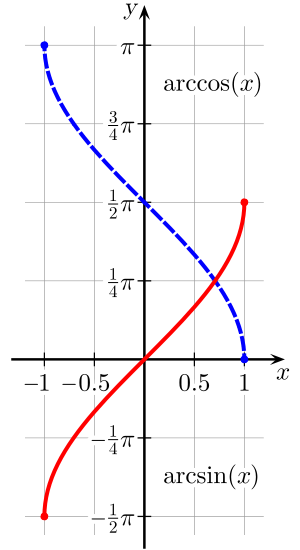
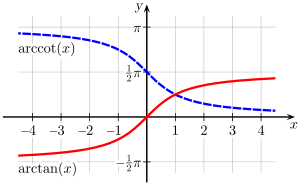
De arcsinusfunctie en arccosinusfunctie in een cartesiaans assenstelsel.

De arctangensfunctie en arccotangensfunctie in een cartesiaans assenstelsel.

De arcsecansfunctie en arccosecansfunctie in een cartesiaans assenstelsel.

Cyclometrische functies, arcfuncties of boogfuncties zijn de inverse functies van de goniometrische functies. Er zijn zes van deze functies: de boogsinus (arcsinus), de boogcosinus (arccosinus), de boogtangens (arctangens), de boogcotangens (arccotangens), de boogsecans (arcsecans) en de boogcosecans (arccosecans). De grafieken van deze functies worden bekomen door spiegeling ten opzichte van de rechte y=x van een gepaste beperking van de grafiek van de overeenkomstige goniometrische functies.

Overzicht van de cyclometrische functies

Naam	Notatie	Definitie	Domein	Bereik
Boogsinus	$y=\arcsin(x)$ $y=\mathrm {bgsin} (x)$	$x=\sin(y)$	$-1\leq x\leq 1$	−π/2 ≤ y ≤ π/2
Boogcosinus	$y=\arccos(x)$ $y=\mathrm {bgcos} (x)$	$x=\cos(y)$	$-1\leq x\leq 1$	0 ≤ y ≤ π
Boogtangens	$y=\arctan(x)$ $y=\mathrm {bgtan} (x)$	$x=\tan(y)$	$-\infty \leq x\leq \infty$	−π/2 < y < π/2
Boogcotangens	$y=\operatorname {arccot}(x)$ $y=\mathrm {bgcot} (x)$	$x=\cot(y)$	$-\infty <x<\infty$	0 < y < π
Boogsecans	$y=\operatorname {arcsec}(x)$ $y=\mathrm {bgsec} (x)$	$x=\sec(y)$	$-\infty <x<-1$ of $1<x<\infty$	$0\leq y<{\tfrac {1}{2}}\pi$ of ${\tfrac {1}{2}}\pi <y<\pi$
Boogcosecans	$y=\operatorname {arccsc}(x)$ $y=\mathrm {bgcsc} (x)$	$x=\csc(y)$	$-\infty <x<-1$ of $1<x<\infty$	$0\leq y<{\tfrac {1}{2}}\pi$ of ${\tfrac {1}{2}}\pi <y<\pi$

Verbanden

Complementaire hoeken

$\arccos x={\frac {\pi }{2}}-\arcsin x$

$\operatorname {arccot} x={\frac {\pi }{2}}-\arctan x$

$\operatorname {arccsc} x={\frac {\pi }{2}}-\operatorname {arcsec} x$

Tegengestelde hoeken

$\arcsin(-x)=-\arcsin x$

$\arccos(-x)=\pi -\arccos x$

$\arctan(-x)=-\arctan x$

$\operatorname {arccot}(-x)=\pi -\operatorname {arccot} x$

$\operatorname {arcsec}(-x)=\pi -\operatorname {arcsec} x$

$\operatorname {arccsc}(-x)=-\operatorname {arccsc} x$

Identiteiten

De hieronder voorgestelde identiteiten met wortels, zijn enkel de wortels van positieve reële getallen (oftewel positieve imaginaire getallen als de wortel negatief is).

Uitgaande van de relatie

$\tan {\frac {\theta }{2}}={\frac {\sin \theta }{1+\cos \theta }}$,

verkrijgt men:

$\arcsin x=2\arctan {\frac {x}{1+{\sqrt {1-x^{2}}}}}$

$\arccos x=2\arctan {\frac {\sqrt {1-x^{2}}}{1+x}}$, als $-1<x\leq 1$

$\arctan x=2\arctan {\frac {x}{1+{\sqrt {1+x^{2}}}}}$

Verder geldt:

$\arcsin x=\operatorname {arccsc} {\frac {1}{x}}$

$\arccos x=\operatorname {arcsec} {\frac {1}{x}}={\frac {\pi }{2}}-\arcsin x$

$\arctan x=\operatorname {arccot} {\frac {1}{x}}$

$\operatorname {arcsec} x=={\frac {\pi }{2}}-\operatorname {arccsc} x$

Logaritmische vormen

Deze functies kunnen ook aan de hand van complexe logaritmen uitgedrukt worden:

${\begin{aligned}\arcsin x&{}=-i\,\ln \left(i\,x+{\sqrt {1-x^{2}}}\right)\\\arccos x&{}=-i\,\ln \left(x+{\sqrt {x^{2}-1}}\right)={\frac {\pi }{2}}\,+i\ln \left(i\,x+{\sqrt {1-x^{2}}}\right)\\\arctan x&{}={\frac {i}{2}}\left(\ln \left(1-i\,x\right)-\ln \left(1+i\,x\right)\right)\\\operatorname {arccot} x&{}={\frac {i}{2}}\left(\ln \left(1-{\frac {i}{x}}\right)-\ln \left(1+{\frac {i}{x}}\right)\right)\\\operatorname {arcsec} x&{}=-i\,\ln \left({\sqrt {{\frac {1}{x^{2}}}-1}}+{\frac {1}{x}}\right)=i\,\ln \left({\sqrt {1-{\frac {1}{x^{2}}}}}+{\frac {i}{x}}\right)+{\frac {\pi }{2}}\\\operatorname {arccsc} x&{}=-i\,\ln \left({\sqrt {1-{\frac {1}{x^{2}}}}}+{\frac {i}{x}}\right)\end{aligned}}$

Zie ook

• Goniometrische functie
• Lijst van goniometrische identiteiten