Demping

impulsrespons van massa-veersystemen met vier verschillende dempingsfactoren

overbrengingsverhouding van massa-veersystemen met vier verschillende dempingsfactoren

In het algemene spraakgebruik is demping de reductie van de sterkte van een of ander verschijnsel. Dat kan bijvoorbeeld geluiddemping zijn, of het toepassen van een sordino bij een strijkinstrument of een demper bij bepaalde blaasinstrumenten. Meer specifiek wordt van demping gesproken wanneer de sterkte van een trilling wordt afgeremd. Demping wordt bewust toegepast om de negatieve effecten van resonantie tegen te gaan. In de mechanica door schokdempers en in de elektronica door weerstanden.

Mechanica

Elk massa-veersysteem, zoals een gewicht dat aan een veer hangt, heeft ten minste één eigenfrequentie, het ritme waarin het gewicht zal bewegen nadat het eenmaal is aangestoten. Wordt op het gewicht een kracht uitgeoefend met dezelfde frequentie, dan zal de uitwijking steeds groter worden. In veel praktische toepassingen is dit verschijnsel ongewenst, denk bijvoorbeeld aan een afgeveerd voertuig. In zulke gevallen is demping nodig.

Demping in de mechanica betekent het afremmen van bewegingen, waarbij de energie van die beweging wordt omgezet in bijvoorbeeld warmte. De dempingskracht kan onafhankelijk zijn van de bewegingssnelheid, zoals bij de droge wrijving in een samengestelde bladveer, maar doorgaans leveren dempers een kracht die evenredig is met de snelheid. In een massa-veersysteem heeft zo'n demper vooral effect bij snelle verplaatsingen die bijvoorbeeld optreden bij resonantie.

De onderdrukking van resonantie is afhankelijk van de dempingsfactor ($\beta$). De overdrachtsfunctie van een gedempt massa-veersysteem is:

$G(s)={\frac {K}{{\frac {s^{2}}{\omega _{0}^{2}}}+2\beta {\frac {s}{\omega _{0}}}+1}}$

Overbrengingsverhouding (kracht-verplaatsing) als functie van de frequentie:

$|G(i\omega )|={\frac {K}{\sqrt {{\big (}1-{\frac {\omega ^{2}}{\omega _{0}^{2}}}{\big )}^{2}+{\big (}{\frac {2\beta \omega }{\omega _{0}}}{\big )}^{2}}}}$

Hierin is

$\beta ={\frac {c}{2{\sqrt {mk}}}}$

$\omega _{0}={\sqrt {\frac {k}{m}}}$

$K={\frac {1}{k}}$

Met $\omega$ de frequentie in rad/s, $m$ de massa in kg, $k$ de veerconstante in N/m en $c$ de dempingsfactor in Ns/m.

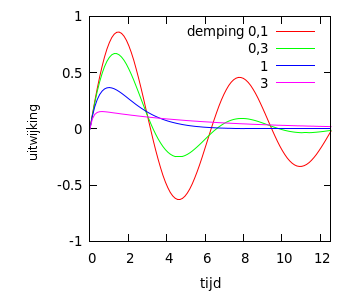
Een dempingsfactor van 1 heet kritische demping, de gedempte slingering heet dan een aperiodieke beweging. Hierbij staat een eenmaal aangestoten massa-veersysteem eerder stil dan bij een hogere of lagere factor. Bij een hogere factor beweegt de massa langzamer naar de uitgangssituatie, bij een lagere factor is er doorschot: de massa slingert (met steeds kleinere amplitude) om de evenwichtspositie. De frequentie van deze slingering ligt iets lager dan de ongedempte resonantiefrequentie:

$\omega _{1}=\omega _{0}{\sqrt {1-\beta ^{2}}}.$

Elektronica

RLC-kring analoog aan demper-massa-veer

In de elektronica bestaat een analogon van het massa-veersysteem in de vorm van een zogenaamde LC-kring. Door aan de parallel geschakelde smoorspoel en condensator nog een weerstand toe te voegen ontstaat demping. De dempingsfactor is omgekeerd evenredig met de weerstandswaarde (dus evenredig met de geleidbaarheid):

$\alpha ={1 \over 2RC}$

Zie ook

• Dempingsfactor (luidspreker)
• Geluidsabsorptie
• Schokdemper
• Tegenkoppeling

Bronnen, noten en/of referenties