Koord om de aarde-puzzel

De lengte toegevoegd aan de omtrek (blauw) is alleen afhankelijk van de extra straal (rood) en niet van de oorspronkelijke omtrek (grijs)

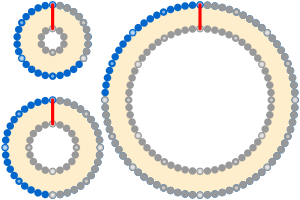
De koord om de Aarde-puzzel (en: string girdling Earth) is een wiskundige puzzel met een contra-intuïtieve oplossing. Het uitgangspunt van deze puzzel is een touw dat strak om de evenaar van een perfect bolvormige aarde gewikkeld is. De puzzel kent twee varianten.

In de eerste variant van de puzzel wordt dit touw opgerekt tot het een meter boven de grond gespannen is. De vraag is dan hoeveel langer dit touw is ten opzichte van het oorspronkelijke op de evenaar gespannen touw.

In de tweede variant van de puzzel wordt een meter toegevoegd in het originele touw, waarna dit touw opgetild en strak over de evenaar gespannen wordt. De vraag is de dan verkregen hoogte van het touw ten opzichte van de aarde. Past hieronder een auto, een kat of een dun mes?

Oplossing

Eerste variant: Omdat het touw over de hele 40.000 km (lengte van evenaar) omhoog moet worden gebracht, zou je enkele kilometers extra touw kunnen verwachten. Verrassend genoeg is het antwoord 2π meter ofwel ongeveer 6,3 meter.

Tweede variant: aangezien een meter bijna verwaarloosbaar is vergeleken met de 40.000 kilometer omtrek, kan de eerste reactie zijn dat de nieuwe positie van het touw ten opzichte van de evenaar niet zal verschillen van de oorspronkelijke positie die het oppervlak omhelst. Het antwoord is dat de hoogte 1/2π meter is ofwel ongeveer 16 centimeter en dus een kat makkelijk door de opening zal gaan.

Visueel analoog met een vierkant

Nog verrassender is mogelijk dat de grootte van de bol of cirkel waarrond het touw is gespannen niet relevant is, en zo groot kan zijn als je maar wilt, het kan de grootte van een atoom zijn, van een basketbal en zelfs van het melkwegstelsel — het resultaat hangt alleen af van hoeveel het touw wordt opgetild. Dit is beter te begrijpen als je de cirkel verandert in een vierkant: ongeacht de grootte van het vierkant, de toegevoegde omtrek zal de som van de vier blauwe bogen zijn, een cirkel met dezelfde straal als de offset.

Bewijsvoering

Het vraagstuk zonder getallen, maar met variabelen: als c de omtrek van de aarde is, r de straal van de aarde, Δ c de toegevoegde touwlengte en Δ r de toegevoegde straal; en als een cirkel met straal R en een omtrek van 2πR heeft, dan geldt:

${\begin{aligned}c+\varDelta c&=2\pi (r+\varDelta r)\\2\pi r+\varDelta c&=2\pi r+2\pi \varDelta r\\\varDelta c&=2\pi \varDelta r\\\therefore \;\varDelta r&={\frac {\varDelta c}{2\pi }}\end{aligned}}$

In de praktijk

De gelijkmatig verspringende startlijnen op een atletiekbaan.

Het kenmerk dat het afstandsverschil niet verandert ongeacht de omtrek, wordt toegepast op atletiekbanen waar de startplaatsen op de loopbanen op gelijke interval van elkaar liggen en ze zo allemaal op dezelfde afstand van de finishlijn liggen. Deze intervallen zijn gelijk aan 2π maal de breedte van de loopbanen. Dit is dus ongeacht of de omtrek van de binnenste baan een lengte heeft van de gewoonlijke 400 meter of zo groot als een sterrenstelsel is.

Zie ook

• Visuele calculus, een intuïtieve manier om dit soort problemen op te lossen, oorspronkelijk toegepast op het vinden van het gebied van een ring, alleen gegeven de koordlengte.
• Napkin ring problem, een ander contra-intuïtief probleem waarbij de straal van een bol irrelevant is.