Spiraal van Ulam

De spiraal van Ulam is een spiraal van de natuurlijke getallen waarbij de priemgetallen gemarkeerd zijn. Het blijkt dan, dat de priemgetallen in bepaalde diagonale patronen voorkomen. De spiraal werd ontdekt door de wiskundige Stanisław Marcin Ulam in 1963.
De spiraal[bewerken | brontekst bewerken]
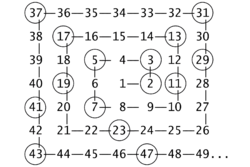
Tijdens een wetenschappelijke bijeenkomst tekende Ulam uit verveling een rooster in de vorm van een spiraal, waarop hij de natuurlijke getallen neerzette met het getal 1 in het midden:
Hij markeerde vervolgens de priemgetallen:
Hij zag, tot zijn verbazing, dat de priemgetallen de neiging hebben om zich op diagonalen van de spiraal te bevinden. De diagonalen zijn ook zichtbaar wanneer er heel veel getallen in een spiraal worden geplaatst. Het opvallende is, dat priemgetallen zich meer op bepaalde diagonalen bevinden dan op andere. Het patroon is ook zichtbaar wanneer men met een ander getal begint.[1] De reden waarom deze patronen ontstaan is nog niet bekend.
Ulams ontdekking was dermate belangwekkend, dat de spiraal op de voorkant van de Scientific American van maart 1964 werd afgebeeld. In die editie stond een artikel over de spiraal van Martin Gardner getiteld Mathematical Recreations: The Remarkable Lore of the Prime Number.[1]
Kenmerken[bewerken | brontekst bewerken]
Het bestaan van deze diagonalen geeft aan dat er rijen van priemgetallen gegenereerd kunnen worden met de volgende functie :
- , waarbij .[1]
De door Leonhard Euler ontdekte formule
die priemgetallen oplevert voor is zichtbaar op de diagonaal als men begint met het getal 41 in het midden.[1]

Ook de formule
is ontdekt door Euler; deze levert priemgetallen op voor .
Varianten[bewerken | brontekst bewerken]

De spiraal van Sacks is een variant van de spiraal van Ulam. Deze spiraal werd in 1994 gemaakt door Robert Sacks. Op deze spiraal worden de getallen, beginnend bij 0, op een Archimedes-spiraal geplaatst in plaats van de vierkante spiraal die Ulam gebruikte.
Externe links[bewerken | brontekst bewerken]
- (en) Prime Spiral op MathWorld
- https://www.ulamspiralmethod.com, website bedoeld voor toelichting aangaande de diagonale oriëntaties & de fragmentarische staat van de rijen van nummers in de Ulam spiraal.
Bronnen, noten en/of referenties
|