Stelling van Viviani

De som l + m + n van de verschillende lengtes is gelijk aan de hoogte van de driehoek.

De stelling van Viviani is een stelling uit de meetkunde vernoemd naar Vincenzo Viviani. Ze stelt dat in een gelijkzijdige driehoek voor een punt in de driehoek, de som van de minimale afstanden naar de drie zijden gelijk aan de hoogte van de driehoek is.

De stelling is uit te breiden naar regelmatige veelhoeken. Hierbij geldt dat de som van de minimale afstanden naar elk van de zijden niet afhankelijk is van het gekozen punt (binnen het figuur). Het omgekeerde is ook waar: wanneer de som van de minimale afstanden naar elk van de zijden van een veelhoek, dan is het een regelmatige veelhoek.

Bewijs

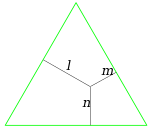
De stelling kan eenvoudig worden bewezen door de oppervlakten van de driehoeken binnen de totale driehoek te bekijken. Noem ABC de gelijkzijdige driehoek, waarbij h de hoogte en z de lengte van elk van de zijden. Stel P een punt binnen de driehoek en l, m en n de minimale afstanden van het punt P naar elk van de zijden. Dan geldt voor de oppervlakte S(ABC) van de driehoek ABC:

$S(ABC)=S(ABP)+S(ACP)+S(BCP),\,$

${\frac {zh}{2}}={\frac {zl}{2}}+{\frac {zm}{2}}+{\frac {zn}{2}},$

$h=l+m+n\,$

zoals te bewijzen was.

Bronnen, noten en/of referenties