Hexagonaal kristalstelsel
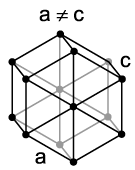
Het hexagonale kristalstelsel is een type kristalstelsel. Er is binnen het hexagonale kristalstelsel een bravaistralies, dus is er in dit geval geen verschil tussen stelsel en bravaistralie. De hexagonale dichtste stapeling valt hieronder. Mineralen met een hexagonale structuur zijn onder meer cadmium en magnesium.
Het hexagonale kristalstelsel telt zes puntgroepen: 6, 6/m, 6 mm, 6/mmm, 622 en 6m2.
Een hexagonaal kristalrooster[bewerken | brontekst bewerken]
Als een tralie zich herhaalt in dezelfde stand, in drie onafhankelijke richtingen, zodat er een groot rooster ontstaat van tralies naast elkaar, en er op ieder traliepunt een atoom of ion wordt ingevuld, noemt men het resultaat een hexagonaal kristalrooster. De atomen of ionen hebben zich dan op de manier gerangschikt als te zien is in het plaatje met het hexagonale rooster.
De structuur kent vier varianten:
Glijvlakken[bewerken | brontekst bewerken]
Ten opzichte van een materiaal met een kubisch rooster, zoals kubisch vlakgecentreerd en kubisch ruimtelijk gecentreerd, heeft een materiaal met een hexagonaal kristalrooster minder glijvlakken. Om precies te zijn treedt de afschuiving alleen op aan de (001)-vlakken, in de [100]-richting. Door het geringe aantal mogelijkheden in afschuiving is er in hexagonale roosters dan ook meer kans op de vorming van tweelingen. Als een materiaal met een kubisch rooster echter verwarmd wordt boven een bepaalde temperatuur, bij magnesium ligt dit bijvoorbeeld zo rond de 200 °C, zullen ook andere glijvlakken optreden.
Coördinatensysteem[bewerken | brontekst bewerken]
In tegenstelling tot bij kubische roosters geeft het rekenen met drie assen bij hexagonale roosters soms problemen. Om deze problemen te ondervangen kan een vierde as aan het coördinatenstelsel worden toegevoegd. In de praktijk wordt deze vierde as door kristallografen niet echt meer gebruikt sinds de komst van geschikte rekensoftware, maar binnen sommige andere vakgebieden komt het gebruik ervan nog voor. Het coördinatenstelsel kent een z-as en drie assen, en , in het grondvlak. Deze assen zijn ten opzichte van elkaar 120 graden gedraaid.
Het omzetten van een drie-assig coördinatensysteem naar het vier-assige systeem kan met de volgende coördinatentransformaties worden uitgevoerd:
Het getal in de laatste formule is een factor die zodanig gekozen kan worden dat en tot hun kleinste gehele getallen gereduceerd kunnen worden.
Websites[bewerken | brontekst bewerken]
- (en) Universiteit van Cambridge. Slip in HCP metals 1: slip systems. Afschuiving in roosters met dichtste bolstapeling, nadere uitleg op een promotiepagina voor materiaalkunde aan de universiteit



![{\displaystyle [u',v',w']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a81e29385bb81d8e643fd50b5445427839c4ad9)
![{\displaystyle [u,v,t,w]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28cc04370c1a09c3633dab023e8eff4550e13e55)






