Bravaistralie

Een bravaistralie of bravaisrooster is een begrip uit de kristallografie. De bravaistralies zijn de veertien manieren waarop kristalroosters meetkundig kunnen worden beschreven. De veertien tralies zijn in 1848 door de Franse kristallograaf Auguste Bravais bedacht.
Alle vaste stoffen op aarde kunnen op drie manieren voorkomen: kristallijn, amorf of een tussenvorm hiervan. Kristallijne stoffen zijn opgebouwd uit netjes gerangschikte atomen, die samen een kristal vormen. Er zijn verschillende manieren waarop kristallijne stoffen gerangschikt kunnen worden in een kristal en daarmee in verschillende typen kristalroosters. Al deze verschillende kristalstelsels kunnen meetkundig worden beschreven met de veertien tralies van Bravais, die ingedeeld worden naar eenheidscel en naar kristalrooster.
Het principe van de bravaisroosters kan ook in twee dimensies worden gebruikt.
Classificatie: eenheidscellen[bewerken | brontekst bewerken]
Een eenheidscel laat zich beschrijven als een parallellepipedum met assen a, b, c en hoeken α, β en γ. Een complicatie treedt op bij de hexagonale cel, want de drietallige as genereert uit één parallellepipedum een hexagonaal prisma als eenheidscel met de puntsymmetrie van het kristal.
Indeling naar locatie en aantal van de traliepunten[bewerken | brontekst bewerken]
De eenheidscellen zijn als volgt ingedeeld naar plaats en aantal traliepunten in de cel:
- P: primitief, één traliepunt op de top van de cel, geen extra traliepunten.
- S: grondvlakgecentreerd, 2 traliepunten, het extra traliepunt op een van de drie grondvlakken. Men kan nader onderscheid maken naar vlak:
- A: het extra traliepunt op het celvlak A gedefinieerd door de assen b en c.
- B: het extra traliepunt op het celvlak B gedefinieerd door de assen a en c
- C: het extratraliepunt op het celvlak C gedefinieerd door de assen a en b
- F: vlakgecentreerd, 4 traliepunten, met de extra traliepunten op ieder van de drie grondvlakken A, B en C.
- I: ruimtelijkcentreerd, 2 traliepunten, het extra traliepunt in het centrum van de cel
- R: twee mogelijkheden: romboëdrisch, dan is het een primitieve cel; of hexagonaal, dan bevat het drie traliepunten per cel. Ook hier wordt de complicatie veroorzaakt door de drietallige rotatie-as.
P, S, F, I en R worden als notatiesymbolen voor bravaistralies gebruikt.
Voorbeeld[bewerken | brontekst bewerken]
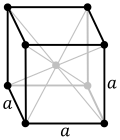
Hiernaast is ter illustratie een kubisch ruimtelijk gecentreerde eenheidscel, ofwel type I, gegeven. Deze heeft de volgende kenmerken:
- De cel is kubisch, ofwel de assen a, b en c zijn gelijk, en de hoeken zijn allen 90°
- De cel is ruimtelijk gecentreerd, ofwel er bevindt zich een traliepunt midden in de cel
- De eenheidscel heeft twee traliepunten;
- Het ene traliepunt zit in het midden van de cel
- Het andere traliepunt zit op het hoekpunt punt (0,0,0) van de cel. Alle andere hoekpunten zijn in een rooster in feite het punt (0,0,0) van de naburige cellen. Ieder hoekpunt van de cel wordt door 8 buren gedeeld, waardoor elk van de 8 hoekpunten voor 1/8 tot de cel behoort.
Overige afbeeldingen zijn verderop in dit artikel te vinden.
Classificatie: kristalstelsels, kristalroosters en kristalfamilies[bewerken | brontekst bewerken]
Kristallen zijn op grond van hun morfologische eigenschappen ingedeeld in kristalstelsels. Er zijn 7 kristalstelsels gedefinieerd op grond van de waarden van de assen a, b, c en hoeken α, β en γ.
De zeven kristalstelsels zijn als volgt ingedeeld:
- triklien - a, b, c, α, β, γ willekeurig
- monoklien - a, b, c, β willekeurig, α = γ = 90°
- orthorombisch - a, b, c willekeurig, α = β = γ = 90°
- tetragonaal - a = b, c willekeurig, α = β = γ = 90°
- trigonaal - a = b = c, α = β = γ
- hexagonaal - a = b, c willekeurig, α = β = 90° γ = 120°
- kubisch - a = b = c, α = β = γ = 90°
Er zijn ook zeven kristalroosters. Op het eerste gezicht lijkt het dat men de kristalroosters als meetkundige abstracties een-eenduidig kan identificeren met de kristalstelsels. Echter, ook hier zorgt in het geval van het trigonale kristalstelsel de drietallige as voor complicaties. Een trigonaal stelsel kan zowel gebaseerd zijn op een hexagonaal prisma als op een parallellepipedum; in het eerste geval heet het rooster hexagonaal en is het stelsel trigonaal(-hexagonaal); in het tweede geval heet het rooster romboëdrisch en is het stelsel trigonaal(-romboëdrisch). De zeven kristalroosters stemmen weer wel overeen met de bravaistralies van de zeven primitieve cellen.
Kristalfamilies worden door hun interne symmetrie gekenmerkt. De zes kristalfamilies zijn:
- kubisch, symbool: c
- hexagonaal, symbool: h
- tetragonaal, symbool: t
- orthorombisch, symbool: o
- monoklien, symbool: m
- triklien, = asymmetrisch, symbool: a.
c, h, t, o, m en a worden in de notatie voor de bravaistralies gebruikt als voorvoegsels bij P, C, I, F en R.
Er zijn maar zes kristalfamilies. Dit komt doordat de hexagonale en trigonale kristalstelsels samen de éne hexagonale kristalfamilie vormen en ook de hexagonale en romboëdrische roosters samen dezelfde éne hexagonale kristalfamilie vormen.
Classificatie: onderling verband met bravaistralies[bewerken | brontekst bewerken]
Onderstaande tabel geeft het onderlinge verband weer tussen kristalfamilies, bravaistralies, kristalroosters en kristalstelsels. In de tabel zijn tevens opgenomen de bijbehorende 32 kristallografische puntgroepen in de Internationale notatie of Hermann-Mauguinnotatie. Dit is nuttig, omdat de combinatie van bravaistralies en puntgroepen de 230 ruimtegroepen oplevert.
De complicatie hexagonaal - trigonaal - romboëdrisch laat zich met deze tabel goed verduidelijken. De tabel maakt onder meer zichtbaar dat het trigonale stelsel overeenkomt met één verzameling puntgroepen, maar met twee kristalroosters en twee bravaistralies, hP en hR, en dat de éne hexagonale bravaistralie hP overeenkomt met twee kistalstelsels.
| kristalfamilie | bravaistralie | kristalrooster | kristalstelsel | bijbehorende puntgroepen, Internationale notatie |
| kubisch | cP, cF, cI | kubisch | kubisch | 23, m3, 432, 43m, m3m |
| hexagonaal | hP | hexagonaal | hexagonaal | 6, 622, 6mm, 6/m, 6/mmm, 6, 62m |
| hexagonaal | hP | hexagonaal | trigonaal | 3, 32, 3m, 3, 3m |
| hexagonaal | hR | rhomboëdrisch | trigonaal | 3, 32, 3m, 3, 3m |
| tetragonaal | tP, tI | tetragonaal | tetragonaal | 4, 4, 422, 4mm, 42m, 4/m, 4/mmm |
| orthorombisch | oP, oS, oF, oI | orthorombisch | orthorombisch | 222, mm2, mmm |
| monoklien | mP, mS | monoklien | monoklien | 2, m, 2/m |
| triklien | aP | triklien | triklien | 1, 1 |
De 14 bravaistralies[bewerken | brontekst bewerken]
De 14 bravaistralies staan in onderstaande tabel weergegeven naar type eenheidscel en naar kristalrooster. Het Pearson symbool staat onder iedere bravaistralie. Merk de complicatie in naamgeving voor hexagonaal - trigonaal - romboëdrisch op.
| kristalstelsel | primitief | ruimtelijk gecentreerd | grondvlak gecentreerd | vlakken gecentreerd |
| triklien | 
|
|||
| aP | ||||
| monoklien | 
|

|
||
| mP | mS | |||
| orthorombisch | 
|

|

|

|
| oP | oI | oS | oF | |
| hexagonaal | 
|
|||
| hP | ||||
| trigonaal | 
|
|||
| hR | ||||
| tetragonaal | 
|

|
||
| tP | tI | |||
| kubisch | 
|

|

| |
| primitief kubisch cP | kubisch ruimtelijk gecentreerd cI | kubisch vlakgecentreerd cF |
Bij de bovenstaande afbeeldingen zij opgemerkt dat de drie hoeken van de romboëder aan elkaar gelijk zijn.
Twee dimensies[bewerken | brontekst bewerken]

Er zijn in twee dimensies vijf soorten bravaisroosters. Hun indeling komt overeen met de vijf mogelijke vormen waarin de behangpatroongroepen kunnen worden onderverdeeld:
- m, 1 - p2, parallellogrammen
- o, 2 - pmm, rechthoeken
- o, 3 - cmm, ruiten
- h, 4 - p6m, dubbele gelijkzijdige driehoeken
- t, 5 - p4m, vierkanten
Vectoren[bewerken | brontekst bewerken]
Ten gevolge van het repetitieve karakter van de roosterstructuren die volgen uit deze tralies, is het gebruik van vectoren in kristallografische problemen zeer nuttig, daarom werden door Auguste Bravais ook kristallografische richtingen voorgesteld.
Bronnen, noten en/of referenties
|
