Stelling van Steiner
De stelling van Steiner is een stelling waarmee het traagheidsmoment van een voorwerp berekend kan worden. De stelling is genoemd naar de Zwitserse wiskundige Jakob Steiner. De stelling is ook bekend als het Huygens-Steiner-theorema.
Tabellen met traagheidsmomenten geven doorgaans enkel formules voor die traagheidsmomenten ten opzichte van een vaste as door het massacentrum. Bij het bestuderen van de rotatie is echter het traagheidsmoment ten opzichte van de rotatieas nodig.
Met de stelling van Steiner kan het traagheidsmoment ten opzichte van een as die niet door het massacentrum loopt, maar wel evenwijdig aan deze door het massacentrum, als volgt berekend worden:
Hierin is:
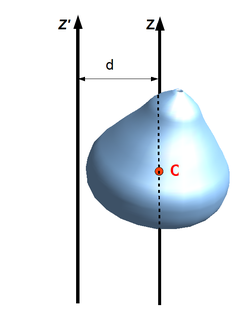
- de afstand van het massacentrum tot de beschouwde as dus de afstand tussen beide assen.
- de massa van het voorwerp.
Voor het oppervlaktetraagheidsmoment geldt een analoge stelling: de massa moet vervangen worden door de oppervlakte:
Bewijs[bewerken | brontekst bewerken]
Als het traagheidsmoment gegeven is ten opzichte van een z-as en gevraagd wordt ten opzichte van een evenwijdige z'-as, dan kan voor elke puntmassa in het systeem geschreven worden dat, in een vlak loodrecht op de assen, de positie ten opzichte van de z'-as gegeven is als:
Hierbij bezitten de vectoren en alleen een x- en y-component en geen z-component.
Het traagheidsmoment ten opzichte van de z'-as is dan:
Oftewel
De term
indien de z-as door het massacentrum gaat. In projectie wordt dit immers
en dit is typisch voor het massacentrum als de posities ten opzichte van het massacentrum bepaald worden. De laatste term is het traagheidsmoment ten opzichte van deze z-as. De formule wordt dus, met m de totale massa:












