Betrouwbaarheidsinterval
Een betrouwbaarheidsinterval is in de statistiek een intervalschatting voor een parameter. In tegenstelling tot een puntschatting geeft een betrouwbaarheidsinterval een heel interval van betrouwbare waarden (schattingen) van de parameter. Een betrouwbaarheidsinterval is een realisatie van een stochastisch interval, dat overigens zelf ook met betrouwbaarheidsinterval wordt aangeduid. De ondergrens en de bovengrens van het stochastische interval zijn stochastische variabelen, die dus bij elke herhaling van het experiment een (mogelijk) andere waarde aannemen. De te schatten parameter daarentegen heeft een, weliswaar onbekende, maar vaste waarde. Van alle realisaties van het interval zullen sommige de parameter wel bevatten, maar sommige ook niet. Hoe groter de betrouwbaarheid, hoe "vaker" het interval de parameter bevat. De kans dat een waargenomen interval de parameter bevat, heet de betrouwbaarheid van het interval. De onder- en de bovengrens worden berekend uit de steekproefgegevens, en wel zo dat er een sterk vermoeden is dat de echte waarde van de populatieparameter zich ertussen bevindt.
Definitie[bewerken | brontekst bewerken]
De stochastische variabelen vormen een steekproef uit een verdeling met onbekende parameter . Als voor de steekproeffuncties en geldt:
- ,
heet het (stochastische) interval een betrouwbaarheidsinterval voor met betrouwbaarheid of een -betrouwbaarheidsinterval. Hierin is de parameter zelf geen stochastische variabele. Voor de realisaties en van respectievelijk en geldt dezelfde kansuitspraak uiteraard niet. Men zegt:
- "met betrouwbaarheid geldt: ".
Als de grenzen van het betrouwbaarheidsinterval uit de steekproef kunnen worden berekend, zijn het dus steekproeffuncties en daarom zelf ook stochastische variabelen.
Interpretatie[bewerken | brontekst bewerken]
Wat betekent een uitspraak: "met betrouwbaarheid 95% ligt de parameter in het waargenomen interval "?
Gezien de definitie houdt dit in dat in 95% van de keren dat het interval op dezelfde manier wordt waargenomen, de parameter in het gevonden interval ligt. De parameter heeft steeds dezelfde onbekende waarde, maar iedere keer wordt een (meestal) ander interval waargenomen. In een grote serie waargenomen intervallen zullen van de intervallen ruwweg 95% de parameterwaarde bevatten.
Of het gevonden betrouwbaarheidsinterval de parameter bevat, blijft in het algemeen onbekend. De parameter ligt er wel of ligt er niet in. Het is dus foutief te zeggen dat met kans 95% de parameter in het gevonden interval ligt.
Voorbeelden[bewerken | brontekst bewerken]
Voorbeeld 1: Verkiezingen[bewerken | brontekst bewerken]
Om een beeld te krijgen van de opkomst bij de naderende verkiezingen, is een enquête onder 1000 aselect gekozen stemgerechtigden gehouden. Van deze steekproef zeiden 700 ondervraagden te zullen gaan stemmen. Het opkomstpercentage is natuurlijk een nog onbekende parameter . Een voor de hand liggende (punt)schatting van is: 0,70. Maar het kan ook wat meer of minder zijn. Mogelijk 0,75 of 0,60. Is het aannemelijk dat het 0,50 zou zijn? Om deze vraag te beantwoorden zoekt men een interval , waarvan met een zekere mate van betrouwbaarheid gezegd kan worden dat daarin zal liggen. Met 100%-betrouwbaarheid kan men zeggen dat tussen 0 en 1 zal liggen, maar dat geeft geen informatie. Maar wat is de betrouwbaarheid van het interval [0,65; 0,75]? En hoe moeten de grenzen worden gekozen, als een betrouwbaarheid van 95% gewenst is?
Noem het aantal stemgerechtigden die zeggen te gaan stemmen. is een stochastische variabele met een binomiale verdeling met parameters en kans dat iemand gaat stemmen. Voor de steekproeffuncties:
en
- ,
waarin de steekproeffractie is, geldt:
Het interval is dus een 0,95-betrouwbaarheidsinterval voor . Omdat voor de waarde 700 gevonden is, kunnen de realisaties en van respectievelijk en berekend worden:
en
Men zegt daarom dat met betrouwbaarheid (let wel: niet met kans) 0,95 geldt dat .
Voorbeeld 2: Kuipjes vullen[bewerken | brontekst bewerken]
Een machine vult kuipjes margarine en is zo ingesteld dat in elk kuipje 250 gram margarine moet komen. Natuurlijk is het niet mogelijk om ieder kuipje met precies 250 gram te vullen. Het vulgewicht is een stochastische variabele , waarvan wordt aangenomen dat die een normale verdeling heeft met verwachting en, voor de eenvoud, bekende standaardafwijking gram. Om de afstelling van de machine te controleren neemt men een steekproef van aselect gekozen kuipjes en weegt die. De gewichten aan margarine zijn , een aselecte steekproef van .
Om alleen maar een indruk te krijgen van de verwachting , is het voldoende een schatting te geven. Het steekproefgemiddelde
is daarvoor geschikt. Maar kunnen er ook grenzen bepaald worden waartussen de parameter met een zekere waarschijnlijkheid ligt? Is er een betrouwbaarheidsinterval voor ?
De gewichten , die in de steekproef zijn gemeten, hebben een gemiddelde van:
- gram.
Dat is een min of meer toevallige waarde. Het had ook 250,4 of 251,1 gram kunnen zijn. Een waarde van 280 gram is daarentegen weer onwaarschijnlijk. Er is een heel interval rond het waargenomen gemiddelde van 250,2 met schattingen die ook betrouwbaar zijn, dat wil zeggen waarvan tamelijk zeker is dat de parameter in dat interval ligt. Tamelijk zeker, want absoluut zeker is alleen het interval (0,∞), maar dat is triviaal.
In ons geval kunnen de grenzen bepaald worden door te bedenken dat het steekproefgemiddelde van een normaal verdeelde steekproef, zelf ook normaal verdeeld is, met dezelfde verwachting , maar met standaardafwijking gram. Het gestandaardiseerde gemiddelde is:
- ,
dat zelf van afhangt, maar standaardnormaal is verdeeld, dus met een verdeling onafhankelijk van de te schatten parameter . Er is daarom een getal , onafhankelijk van , zodanig dat het gestandaardiseerde gemiddelde met een voorgeschreven kans tussen en ligt. De betrouwbaarheid geeft aan hoe betrouwbaar het interval gevonden wordt. Voor de keuze krijgt men:
Het getal volgt uit:
- ,
dus , en er geldt:
De interpretatie hiervan is: met kans 0,95 wordt een interval gevonden met stochastische grenzen
en
- ,
waar tussenin ligt.
Elke keer dat de metingen worden herhaald, vindt men een andere waarde voor het steekproefgemiddelde . In 95% van de gevallen zal tussen de met dit gemiddelde berekende grenzen liggen, in 5% van de gevallen echter ook niet. Het actuele betrouwbaarheidsinterval wordt berekend door de waarden van de gevonden gewichten in te vullen. Het 0,95-betrouwbaarheidsinterval voor is:
In de onderstaande figuur zijn 50 realisaties van een betrouwbaarheidsinterval met betrouwbaarheid 95% voor een onbekende parameter aangegeven.
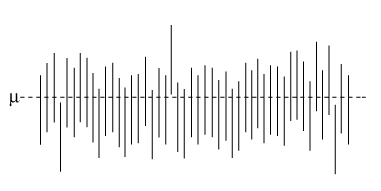
De meeste, in doorsnee 95%, van deze intervallen bevatten de parameter. Enkele daarentegen ook niet. In de praktijk hebben we te maken met een van deze intervallen. Welke dat is weten we niet. Toen we de steekproef namen, hadden we een kans van 95% om een interval te vinden waarin zich de parameter bevindt. Daarom zeggen we dat de parameter met betrouwbaarheid 95% in dit interval ligt. Daarmee bedoelen we niets meer dan dat.
Betrouwbaarheidsintervallen bij verschillende verdelingen[bewerken | brontekst bewerken]
Normale verdeling[bewerken | brontekst bewerken]
Laat een aselecte steekproef uit de normale verdeling zijn, het steekproefgemiddelde en de variantie.
Bij bekende variantie wordt een -betrouwbaarheidsinterval voor gegeven door:
- ,
met het -fractiel van de standaardnormale verdeling, dus .
Als niet bekend is, wordt deze geschat, en wordt het -betrouwbaarheidsinterval voor :
- ,
met het -fractiel van de -verdeling.
Een -betrouwbaarheidsinterval voor is:
met en respectievelijk het - en het -kwantiel van de -verdeling.
Exponentiële verdeling[bewerken | brontekst bewerken]
Laat een aselecte steekproef zijn uit de exponentiële verdeling met verwachting en het steekproefgemiddelde.
Een -betrouwbaarheidsinterval voor wordt gegeven door:
- ,
met en respectievelijk het - en het -kwantiel van de -verdeling.
Binomiale verdeling[bewerken | brontekst bewerken]
Laat binomiaal verdeeld zijn met parameters en , en een schatter van .
Voor relatief grote wordt een benaderend -betrouwbaarheidsinterval voor gegeven door:
- ,
met het -kwantiel van de standaardnormale verdeling, dus .
Poissonverdeling[bewerken | brontekst bewerken]
Laat Poisson-verdeeld zijn met verwachtingswaarde . Uit de relatie tussen de verdelingsfuncties van de Poissonverdeling en de chi-kwadraatverdeling kan het volgende -betrouwbaarheidsinterval voor afgeleid worden:
- ,
met het -kwantiel van de -verdeling.
Websites[bewerken | brontekst bewerken]
- (en) Interpreting Confidence Intervals. visualisatie van gesimuleerde betrouwbaarheidsintervallen













![{\displaystyle [p_{\text{onder}},p_{\text{boven}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fe6dac4725200a37df917c29dfe06109e3cf80c)


























































