Lagrange-multiplicator

De term Lagrange-multiplicator is een begrip en techniek uit de wiskunde (en de studie van wiskundige optimalisatie) genoemd naar de wiskundige Joseph Louis Lagrange. De naam verwijst naar een bepaald soort hulpvariabele die bij deze techniek wordt ingevoerd, waarmee zowel de formulering als de oplossing van het optimalisatieprobleem sterk vereenvoudigt.

Uitleg

Afbeelding 1: Zoek de x en y waarvoor de functie $f(x,y)$ maximaal is, en waarvoor de eis $g(x,y)=c$ (weergegeven in het rood) voldaan is.

Men komt vaak optimaliseringsproblemen tegen van de vorm:

maximaliseer de functie $f(x,y)\;$

onder de voorwaarde $g(x,y) = c\;$.

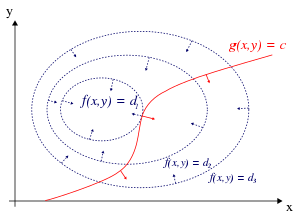
In woorden, we zoeken het punt $(x,y)$ dat op de kromme $g(x,y) = c$ ligt en waarvoor de functie $f$ maximaal of minimaal is. Dit probleem is weergegeven op de afbeeldingen rechts.

Om dit probleem op te lossen voert men een nieuwe variabele $\lambda$ in, de Lagrange-multiplicator, en beschouwt de functie

$\Lambda(x,y,\lambda) = f(x,y) + \lambda \Big(g(x,y)-c\Big).$

Het blijkt nu dat er voor een oplossing $(x, y)$ van het oorspronkelijke probleem, noodzakelijk een λ bestaat waarvoor $(x,y,\lambda)$  een stationair punt is van de functie $\Lambda(x,y,\lambda)$ (ook wel Lagrangefunctie genoemd).

Deze nieuwe formulering van het probleem heeft twee voordelen: ten eerste herleidt dit het oorspronkelijke probleem tot een volkomen standaard en goed bestudeerd probleem (het zoeken naar de stationaire punten van een functie), ten tweede blijken de op te lossen vergelijkingen in deze formulering vaak eenvoudiger dan in de oorspronkelijke verwoording.

Intuïtieve uitleg

Afbeelding 2: Alternatieve weergave van Afbeelding 1. De rode lijn geeft wederom de eis $g(x,y)=c$ weer, en de waarde de functie $f(x,y)$ is nu als hoogte weergegeven. De blauwe lijnen zijn hoogtelijnen, dus lijnen waarlangs de waarde van $f$ constant is. De oplossing is gegeven door de plaats waar de rode lijn raakt aan de blauwe hoogtelijn.

Hierboven werd gesteld dat elke oplossing van het oorspronkelijke variatieprobleem gegeven is door een stationair punt van de Lagrangefunctie $\Lambda$. (Andersom is dit niet waar: niet elk stationair punt van $\Lambda$ geeft een oplossing van het oorspronkelijke variatieprobleem.) Om deze uitspraak intuïtief te begrijpen, kan men de volgende redenering houden. Beschouw de lijnen waarlangs de functie $f$ een constante waarde heeft: $f(x,y) = d$. Als men de functiewaarden van $f$ op de z-as aangeeft, zijn deze lijnen de hoogtelijnen. Er zijn er zo twee getekend op de afbeelding rechts (dat wil zeggen, voor twee verschillende functiewaarden $d_1$ en $d_2$. Stel nu dat we wandelen langs de rode kromme $g(x, y) = c$. Dat is de verzameling punten die aan het vereiste voldoen. In het algemeen zal (gedurende dit wandelen) de waarde van $f$ aan het toe-, dan wel afnemen zijn. Dat wil zeggen dat op die plaatsen de kromme de hoogtelijnen snijdt. Echter, op het punt van de kromme waar $f$ extreem is, verandert de hoogte niet meer (bereikt zijn minimum/maximum), en dus raakt de hoogtelijn daar de kromme $g(x, y) = c$. Aangezien de gradiënt van een functie loodrecht staat op de lijnen waarlangs deze functie constant is, impliceert de vorige zin dat ter hoogte van het gezochte punt ($f(x,y)$ extremaal en $g(x,y)=c$) de gradiënten van $f$ en $g$ evenwijdig zijn. De oplossing van ons probleem heeft dus als bijzondere eigenschap

$\nabla_{x,y} f = \lambda \nabla_{x,y} g$,

waarbij de gradiënt gegeven is door

$\nabla_{x,y} f= \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right)$

en analoog

$\nabla_{x,y} g= \left( \frac{\partial g}{\partial x}, \frac{\partial g}{\partial y} \right)$.

Hier drukt de constante $\lambda$ uit dat de loodrechte vectoren (de gradiënten) evenwijdig zijn, maar niet noodzakelijk even groot zijn/in dezelfde richting staan.

Nu zien we dat de uitspraak in de voorgaande sectie inderdaad steekhoudt. Daar werd gesteld dat de oplossing van het probleem gegeven is door stationaire punten van de Lagrangefunctie, dus punten waarvoor

$\nabla_{x,y,\lambda} \Lambda(x , y, \lambda)=0$.

(de notatie $\nabla_{x,y,\lambda}$ slaat weer op de gradiënt, dus zowel de afgeleiden naar $x$, en naar $y$, als die naar $\lambda$ moeten nul zijn.) Als we de uitdrukking voor de Lagrangefunctie $\Lambda$ invullen, zien we dat de afgeleiden naar $x$ en $y$ impliceren dat

$\nabla_{x,y} f = \lambda \nabla_{x,y} g$.

Dat is precies de bovenstaande uitspraak dat ter hoogte van de oplossing, de loodrechte vectoren op de hoogtelijnen van $f$ en $g$ evenwijdig zijn. Anderzijds, de afgeleide naar $\lambda$ geeft het oorspronkelijke vereiste, namelijk

$g(x, y) = c$.

Dit bevestigt (ten minste intuïtief) dat elke oplossing $(x,y)$ van het oorspronkelijke probleem overeenkomt met een $(x,y,\lambda)$ die voldoet aan $\nabla \Lambda=0$.

Typisch vindt men echter een aantal oplossingen voor $\nabla \Lambda=0$, waarvan dan slechts een of enkele oplossingen voldoen aan het oorspronkelijke probleem. (Dit is analoog aan het zoeken naar extrema van een functie. De punten waar de afgeleide van de functie nul worden zijn lokale extrema, en typisch zijn daarvan slechts een of twee punten globale extrema.)

Eenvoudig voorbeeld

Afbeelding 3: eenvoudig voorbeeld.

We lichten de bovenstaande techniek toe met een eenvoudig voorbeeld.

Stel dat we de functie $f(x,y)=x+y$ willen maximaliseren, gegeven de vereiste $x^2+y^2=1$. Dit wil dus zeggen: zoek het punt op de eenheidscirkel, waarvoor $x+y$ maximaal is. Aangezien de lijnen van constante $x+y$ gegeven zijn door rechtes, met richtingscoëfficiënt $-1$, kan men vrijwel op het eerste gezicht zien dat de raakpunten tussen één van deze hoogtelijnen en de cirkel zijn gegeven door de posities $(\sqrt{2}/2,\sqrt{2}/2)$ en $(-\sqrt{2}/2,-\sqrt{2}/2)$. (Het eerste van de twee komt overeen met het maximum van $f$.)

Laten we dit, puur ter illustratie, oplossen met de bovenstaande techniek.

Noem $g(x,y)-c=x^2+y^2-1$, en stel

$\Lambda(x, y, \lambda) = f(x,y) + \lambda(g(x,y)-c) = x+y + \lambda (x^2 + y^2 - 1)$

Eisen dat de afgeleides $\nabla\Lambda=0$ nul zijn, geeft de volgende vergelijkingen:

$\begin{align} \frac{\partial \Lambda}{\partial x} &= 1 + 2 \lambda x &&= 0, \qquad \text{(i)} \\ \frac{\partial \Lambda}{\partial y} &= 1 + 2 \lambda y &&= 0, \qquad \text{(ii)} \\ \frac{\partial \Lambda}{\partial \lambda} &= x^2 + y^2 - 1 &&= 0, \qquad \text{(iii)} \end{align}$

Zoals altijd is de vergelijking die volgt uit $\partial_\lambda$ de vereiste waarvan we vertrokken.

De eerste twee vergelijkingen impliceren dat $x=y$, en als men dit in (iii) invult, krijgt men $2x^2=1$, of te $x=\pm \sqrt{2}/2$. Dit betekent dat de extremale punten zijn gegeven door $(\sqrt{2}/2,\sqrt{2}/2)$ en $(-\sqrt{2}/2,-\sqrt{2}/2)$. Zoals herhaaldelijk gesteld in de bovenstaande uitleg, is niet elk extremaal van de Lagrange-functie een oplossing van het oorspronkelijke probleem. Hier zochten we het maximum, wat dus overeenkomt met de eerste van deze twee oplossingen.

Betekenis van de multiplicatoren, toepassingen in de economie

Bij veel problemen heeft de concrete waarde van de Lagrange-multiplicator ook een betekenis. Bedenk eerst dat:

$-\frac{\partial \Lambda}{\partial {c}} = \lambda.$

λ zegt dus in welke mate de waarde van het bereikte maximum verandert indien men de eis $g(x,y)=c$ verandert door een andere waarde voor $c$ toe te laten. Een typische situatie in economie waarbij Lagrange-multiplicatoren gebruikt worden is een vraagstuk van de vorm: gegeven een bepaald budget, hoe kunnen we een bepaalde grootheid (het economisch nut) maximaliseren. In dat geval zal (bij het oplossen van het probleem), de waarde van de Lagrange-multiplicator aangeven in welke mate het nut verandert als men het budget aanpast.

Zie ook

• Extremum
• Variatieprincipe

Referenties

• (en) Lagrange-multiplicatoren op de Wolfram-website.
• (en) http://eom.springer.de/L/l057190.htm

(Veralgemenen ook naar de situatie met meerdere opgelegde eisen, wat meerdere Lagrange-multiplicatoren vereist.)

Externe links

• (nl) slides over Functies van meerdere veranderlijken en Lagrange-multiplicatoren.
• (en) Conceptuele inleiding
• (en) Leertekst over Lagrange-multiplicatoren
• (nl) Voorbeeld-oefening uit de economie

Interactief

• (en) Video-les over Langrange-multiplicatoren, toegepast op een concreet voorbeeld uit de economie.