Resultante
Een resultante is in de mechanica de wiskundige vectorsom van twee of meer vectoren, die grafisch grootte en richting aangeven van krachten die tegelijkertijd op een lichaam werkzaam zijn. Ter vereenvoudiging wordt er één enkele virtuele oorzaak berekend die de eigenlijke, op het object inwerkende krachten kan vervangen.
Als meer dan één kracht inwerkt op een voorwerp, zal dat voorwerp als gevolg daarvan een effect ondervinden: het zal al of niet versnellen. Bij krachten die in één vlak liggen, kan dit voorgesteld worden als het effect van één virtuele kracht, de resultante, aangrijpend op een bepaald punt. Dit vormt dan een vervangende, equivalente beschrijving voor de gezamenlijke, inwerkende krachten.
In het volledig algemene driedimensionale geval zal men voor een equivalente beschrijving een resultante, de som van alle krachten, en een resulterend moment t.o.v. een bepaald punt moeten invoeren. Zie hiervoor de link in de laatste alinea.
Mechanica
[bewerken | brontekst bewerken]
In de mechanica kan een kracht grafisch worden voorgesteld als een vector met grootte en richting. De grootte en richting van de resultante van twee krachten kan worden berekend door de vectoren bij elkaar op te tellen. In een tekening, waarin de krachten worden voorgesteld als een pijl, kan dit worden geconstrueerd door het beginpunt van de tweede pijl te verbinden met het eindpunt van de eerste: de som is dan de pijl van het beginpunt van de eerste naar het eindpunt van de verschoven tweede pijl; zie ook parallellogramregel.
Aangrijpingspunt
[bewerken | brontekst bewerken]De resultante van een aantal krachten die op een voorwerp werken, kan een verplaatsing veroorzaken, maar ook een rotatie van dat voorwerp. In alle gevallen zal het massamiddelpunt zo bewegen alsof de resultante daar aangrijpt. Als het aangrijpingspunt van de resultante niet in het massamiddelpunt ligt, mag men deze resultante alleen verplaatsen naar het massamiddelpunt mits men er het moment aan toevoegt van de resultante in haar oorspronkeijke positie t.o.v. het massamiddelpunt. Dit moment, dat men ook kan voorstellen als veroorzaakt door een koppel van krachten, zal nog een rotatie veroorzaken.
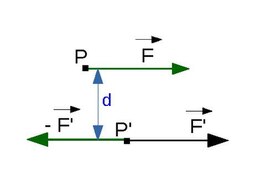
Men kan de noodzaak van een bijkomend moment eenvoudig aantonen. Veronderstel een kracht aangrijpend in een punt P. Men wil deze kracht verplaatsen naar het punt P' dat niet op de drager van die kracht ligt. Men kan dan in P' een kracht gelijk aan invoeren en tegelijkertijd het tegengestelde hiervan. Dit verandert niets aan de situatie want de som van deze twee krachten is nul en ook hun moment is nul. Men kan de drie vectoren nu echter anders opvatten, nl. de vector kan men zien als de verplaatste vector . De twee overige vectoren (in het groen op de figuur) vormen dan een koppel met een moment dat overeenkomt met het moment van in de originele positie ten opzichte van de nieuwe positie.
Edward Routh bedacht in 1893 een grafische oplossing voor de bepaling van het aangrijpingspunt van de resultante:
- bepaal het snijpunt van de twee vectoren;
- trek een cirkel door het gevonden snijpunt en de aangrijpingspunten van de twee vectoren;
- trek een lijn van het snijpunt (1) in de richting van de resultante en bepaal het (andere) snijpunt met de cirkel (2); dit punt is het aangrijpingspunt van de resultante.
Deze procedure kan worden herhaald als er meer dan twee krachten in het spel zijn: de resultante van drie krachten is dan de resultante van de resultante van de eerste twee krachten en de derde kracht.
In feite is deze constructie te ingewikkeld. Een kracht mag immers langs zijn drager (werklijn) verplaatst worden. Beide krachten kunnen dus naar het snijpunt van hun werklijnen verplaatst worden, waar ook resultante aangrijpt.
Bij twee evenwijdige krachten werkt deze constructie niet. De locatie van het aangrijpingspunt wordt dan gegeven door:
Hierin is de lengte van de eerste vector, de lengte van de tweede vector, de afstand tussen de twee aangrijpingspunten en de afstand van het gezochte aangrijpingspunt gerekend vanaf het midden van de twee aangrijpingspunten in de richting van het aangrijpingspunt van de eerste vector.
Voor een meer algemene behandeling met meerdere evenwijdige krachten zie Equivalente vectorsystemen.[1]
Betekenis
[bewerken | brontekst bewerken]Is de resultante met zijn aangrijpingspunt bekend, dan zal een even grote maar in richting tegengestelde kracht met dat aangrijpingspunt op de drager van de resultante de andere krachten precies opheffen zonder een resulterend moment.
Voor een algemene behandeling van het overgaan op een eenvoudiger 'equivalent systeem van krachten' zie Equivalente vectorsystemen.[1]







