Stoptijd
In de kansrekening is een stoptijd in een stochastisch proces een toevallig tijdstip, dat wil zeggen een toevalsvariabele met als waarde een tijdstip, waarvan de realisatie afhangt van een speciale gebeurtenis bij het stochastische proces. Een stoptijd heeft als eigenschap dat kennis van het proces tot en met een gegeven vast tijdstip volstaat om te weten of het toevallige tijdstip tot dan reeds heeft plaatsgehad.
Definitie[bewerken | brontekst bewerken]
Formeel wordt een stoptijd op een kansruimte gedefinieerd ten opzichte van een stijgende rij deel-sigma-algebra's van die geïndexeerd worden door een totaal geordende "tijdstippenverzameling" : voor alle is .
We veronderstellen dat op de tijdstippenverzameling een sigma-algebra gegeven is. In praktische voorbeelden is meestal de verzameling der natuurlijke of niet-negatieve reële getallen, eventueel uitgebreid met het element "oneindig"; dan is deze aanvullende voorwaarde alvast geen probleem.
Een toevalsvariabele heet stoptijd (ten opzichte van de stijgende familie sigma-algebra's) als voor alle
Vaak is de stijgende familie sigma-algebra's, gewoon de informatie over het verleden van een stochastisch proces :
Daarom wordt gesproken van een "stoptijd ten opzichte van een proces".
Voorbeeld[bewerken | brontekst bewerken]
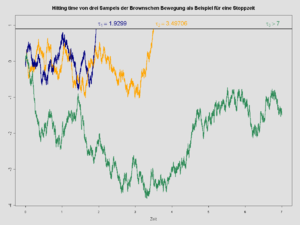
Zij en zij de eendimensionale stochastische wandeling. Voeg aan nog de waarde oneindig toe en spreek arbitrair af dat .
Definieer als het kleinste tijdstip waarop de absolute waarde van het proces de waarde 10 overschrijdt: We spreken af dat het minimum van de lege verzameling oneindig bedraagt.
Dan is een stoptijd, omdat de gebeurtenis kan worden herschreven in termen van het verleden van het proces:
en het rechterlid definieert duidelijk een gebeurtenis die meetbaar is ten opzichte van de stam, voortgebracht door de eerste variabelen van het proces.
Dit is een bijzonder geval van een algemenere klasse stoptijden die inkomtijden heten.
Toepassing[bewerken | brontekst bewerken]
Onder bepaalde voorwaarden is de verwachting van een martingaal, geëvalueerd op een stoptijd, gelijk aan de algemene verwachting van de martingaal. Met behulp van deze intuïtief duidelijke vaststelling worden krachtige resultaten verkregen in de studie van martingalen in het algemeen, en van de brownse beweging in het bijzonder.
Met name de recurrentie van de toevallige wandeling en de brownse beweging in twee dimensies, en hun transiëntie in drie of meer dimensies, wordt het eenvoudigst aangetoond met behulp van stoptijden.



















