Substitutieversleuteling
Substitutieversleuteling is een methode die in de cryptografie wordt gebruikt. De encryptie veronderstelt de aanwezigheid van een verzameling van symbolen, die in de cijfertekst worden gebruikt. Hiervoor kunnen meer symbolen worden gebruikt dan uit het alfabet.
Buiten het vervangen van de letters in de klare tekst is het ook mogelijk combinaties van letters vervangen. Men spreekt in het eerste geval van een eenvoudige substitutie en in het tweede van polygrafische substitutie. Daarnaast bestaat het onderscheid tussen monoalfabetische substitutie, waarbij voor het hele te versleutelen bericht één enkel substitutie-alfabet gebruikt wordt, en polyalfabetische substitutie, waarbij het substitutie-alfabet tijdens de versleuteling verandert.
Men zou de Morsecode als substitutieversleuteling kunnen zien. Morsecode is echter nooit 'geheim' geweest en kan dientengevolge niet in de 'geheim'schriften worden ingedeeld.
Substitutie komt in de literatuur voor, bijvoorbeeld in The Gold-Bug van Edgar Allan Poe, maar ook in Avontuur van de dansende mannen van Sherlock Holmes:
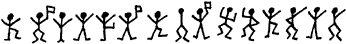
Substitutieversleuteling verschilt van het transpositiecijfer, waar de letters niet worden vervangen, maar alleen anders gerangschikt. Combinaties zijn uiteraard mogelijk.
Monoalfabetische substitutie[bewerken | brontekst bewerken]
Monoalfabetische substitutie vervangt gedurende de hele encryptie elke letter van de klare tekst met een vooraf vastgesteld substituut. Historische voorbeelden hiervan zijn het Caesarcijfer en atbash. Er zijn verscheidene variaties op deze twee methoden en totdat Arabische wiskundigen in de 9e eeuw de techniek van frequentieanalyse ontdekten werden ze als onbreekbaar beschouwd. Behalve de twee genoemde is ook het rozenkruisersgeheimschrift een voorbeeld van monoalfabetische substitutie.
Homofone substitutie[bewerken | brontekst bewerken]
Een belangrijke ontwikkeling om de frequentieanalyse tegen te gaan was de homofone substitutie. Hierbij worden in het versleutelingsalfabet meer symbolen gebruikt dan in het alfabet van de klare tekst. De veel voorkomende letter E kan bijvoorbeeld door drie substituten worden vervangen, bijvoorbeeld de getallen 5, 31 en 57. Veel voorkomende letters krijgen bij homofone substitutie meer substituten dan minder vaak voorkomende. De frequentieverdeling van de cijfertekst wordt als gevolg daarvan 'plat', omdat elk substituut ongeveer even vaak voorkomt.
Een uitgebreidere variant van homofone substitutie is de nomenclatuur.[1] Hier wordt het gebruikt in combinatie met een codeboek waarin veel voorkomende namen en begrippen een eigen substituut krijgen. Een voorbeeld hiervan is het Grote Geheimschrift van Lodewijk XIV.
Polygrafische substitutie[bewerken | brontekst bewerken]
Bij polygrafische substitutie worden de letters in combinatie vervangen in plaats van per letter. Dit was een belangrijke ontdekking tegen frequentieanalyse. De oudst bekende verhandeling van polygrafische substitutie komt uit 1586 beschreven in de furtivis literarum notis van Giambattista della Porta. Felix Delastelle publiceerde over verscheidene polygrafische versleutelingen, onder andere over het bifid- en het trifidcijfer. Een ander bekend voorbeeld van polygrafische subtitutie is het Playfaircijfer.
Polyalfabetische substitutie[bewerken | brontekst bewerken]

Bij polyalfabetische substitutie wordt gebruikgemaakt van verschillende versleutelingsalfabetten, meestal in de vorm van tabellen. De oudst bekende omschrijving van polyalfabetische substitutie stamt uit 1463 en komt van Leon Battista Alberti, omstreeks 1500 gevolgd door een beschrijving in het werk Steganographia van Johannes Trithemius. Een meer complexe manier met een gemengd alfabet werd in 1563 door Giambattista della Porta in zijn De Furtivis Literarum Notis beschreven, maar het bekendste werk aangaande polyalfabetische substitutie komt van Blaise de Vigenère. Zijn Vigenèrecijfer heeft lang bekendgestaan als le chiffre indéchiffrable, Frans voor het onontcijferbare geheimschrift.
|
