Vereniging (verzamelingenleer)

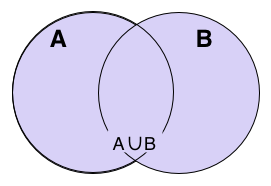
In de verzamelingenleer is de vereniging of unie van een collectie verzamelingen de verzameling die bestaat uit alle elementen van de samenstellende verzamelingen. Zo bestaat de vereniging van de verzamelingen $A$ en $B$ uit alle elementen die tot $A$, $B$ of allebei behoren.

Definitie

De vereniging $A\cup B$ van de verzamelingen $A$ en $B$ is de verzameling die bestaat uit alle elementen van $A$ en van $B$:

$A\cup B=\{x\mid x\in A{\text{ of }}x\in B\}$

De doorsnede en het verschil van twee verzamelingen worden op een overeenkomende manier gedefinieerd.

Voorbeeld

Zij $A=\{1,2,6,10,12\}$ en $B=\{1,2,5,8\},$ dan is $A\cup B=\{1,2,5,6,8,10,12\}.$

Generalisatie

Zij $X$ een willekeurige verzameling en ${\mathcal {F}}$ een familie deelverzamelingen van $X.$ De familie ${\mathcal {F}}$ mag oneindig of zelfs overaftelbaar veel verschillende deelverzamelingen van $X$ bevatten.

De vereniging van ${\mathcal {F}}$ is de deelverzameling van $X$ die bestaat uit alle elementen $x\in X$ die tot minstens één lid van de familie ${\mathcal {F}}$ behoren.

In het bijzonder wordt de vereniging van een lege familie verondersteld leeg te zijn.

De veronderstelling van het bestaan van de universumverzameling $X$ is nodig om paradoxen te vermijden. De vereniging van een willekeurige familie verzamelingen is binnen de axiomatische verzamelingenleer niet gedefinieerd.

Eigenschappen

• De vereniging is een associatieve en commutatieve operatie, dus:

$A\cup (B\cup C)=(A\cup B)\cup C=A\cup B\cup C$

en

$A\cup B=B\cup A$

• Het aantal elementen in de vereniging $\bigcup _{i=1}^{n}V_{i}$ van een $n$ verzamelingen $V_{i}$ is

$|\ \bigcup _{i=1}^{n}V_{i}\ |\ =\ \sum _{i=1}^{n}|\ V_{i}\ |\ -\ \sum _{i<j}^{n}|\ V_{i}\cap V_{j}\ |\ +\ \sum _{i<j<k}^{n}|\ V_{i}\cap V_{j}\ \cap V_{k}\ |\ -\ \cdots \ \pm (-1)^{n+1}\ |\ V_{1}\cap \cdots \ \cap \ V_{n}\ |$

Mediabestanden

Zie de categorie Union (set theory) van Wikimedia Commons voor mediabestanden over dit onderwerp.