Young-tableau

In de representatietheorie is een young-tableau een grafische voorstelling die gebruikt wordt bij de representatie van een symmetrische groep. Ze worden ook toegepast in de combinatoriek en algebraïsche meetkunde. Young-tableaus zijn genoemd naar de Britse wiskundige Alfred Young, die ze in 1900 introduceerde,

Definities

Young-diagram

Young-diagram met vorm [5,4,1], Engelse schrijfwijze

Een young-diagram (ook Ferrersdiagram genoemd) is een eindige verzameling van vakjes of cellen, gerangschikt in rijen die links zijn uitgelijnd, op een zodanige wijze dat het aantal vakjes in een rij nooit kleiner is dat het aantal vakjes in de rij eronder. Het aantal vakjes in de rijen is met andere woorden een niet-stijgende rij.

De opsomming van het aantal vakjes in elke rij bepaalt de vorm van het diagram en vormt een partitie van de verzameling $\{1,\ldots ,n\},$ met $n$ het totaal aantal vakjes in het diagram. Elke rij in het diagram stelt een deelverzameling van de partitie voor.

Een young-diagram wordt traditioneel aangeduid met een Griekse letter $\lambda ,$ de partitie met $[\lambda _{1},\lambda _{2},\ldots ];$ het young-diagram hiernaast dus met $\lambda [5,4,1].$

Een young-diagram kan gespiegeld worden omheen de hoofddiagonaal, waarbij rijen en kolommen worden omgewisseld. Men krijgt dan een nieuw young-diagram, het geconjugeerde diagram. Bijvoorbeeld een diagram met vorm [4,3,3,2] wordt omgezet in het geconjugeerde diagram met vorm [4,4,3,1]. Het geconjugeerde diagram van het hiernaast afgebeelde diagram heeft als vorm [3,2,2,2,1].

Young-diagrammen kan men opvullen. Een opvulling van een diagram is een diagram waarin elk vakje gevuld is met een positief geheel getal (of meer algemeen: met een element uit een verzameling waarop een totale orde is gedefinieerd. Voor de eenvoud gebruikt men doorgaans de positieve gehele getallen 1, 2, 3, ...).

Nota: de hier gebruikte voorstelling van young-diagrammen noemt men de "Engelse" notatie. Er bestaat ook een "Franse notatie", waarin het diagram ondersteboven wordt getekend, met de langste rij onderaan. Dit artikel gebruikt de traditionele Engelse notatie.

Young-tableau

Een standaard young-tableau met n=10 vakjes

Een young-tableau is een opvulling van een young-diagram die aan bepaalde voorwaarden voldoet. Men maakt een onderscheid tussen een semistandaard young-tableau en een standaard young-tableau.

Een semistandaard young-tableau voldoet aan de volgende voorwaarden:

• in elke rij vormen de getallen een niet-dalende rij (elk getal is kleiner dan of gelijk aan het getal rechts ervan)
• in elke kolom vormen de getallen een strikt stijgende rij (elk getal is kleiner dan het getal eronder, als dat bestaat).

Een standaard young-tableau voldoet aan de voorwaarden:

• in elke rij en in elke kolom vormen de getallen een strikt stijgende rij
• alle getallen in het tableau zijn verschillend.

In een standaard young-tableau met $n$ vakjes staan dus de eerste $n$ positieve gehele getallen. In een semistandaard young-tableau kunnen er minder dan $n$ verschillende getallen staan (maar minstens het aantal rijen in het diagram). Het geconjugeerde tableau van een standaard young-tableau is ook standaard.

Scheef young-diagram en young-tableau

Scheef young-tableau bekomen door $\mu [2,1].$ te verwijderen uit $\lambda [5,4,2,2].$

Een scheef young-diagram (Engels: skew) krijgt men als men uit een young-diagram $\lambda$ een ander, kleiner young-diagram $\mu$ in de linkerbovenhoek wegneemt. Het resterende scheve diagram, $\lambda /\mu$ is de verschilverzameling van de vakjes die behoren tot $\lambda$ maar niet tot $\mu$.

Scheve young-tableaus definieert men dan op dezelfde wijze als hierboven: semistandaard als de opeenvolgende getallen in een rij niet-dalend zijn en in een kolom strikt stijgend; standaard als ze zowel in rijen als kolommen strikt stijgend zijn en alle getallen van 1 tot het aantal vakjes in het tableau eenmaal erin voorkomen.

Voor een scheef young-diagram volstaat het niet het aantal vakjes in elke rij op te sommen om de vorm van het diagram te kennen; men moet ook de vorm van het weggelaten diagram kennen. Het diagram hiernaast wordt daarom genoteerd als [5,4,2,2]/[2,1].

Aantallen young-tableaus

Een semistandaard young-tableau kan men aanduiden met $(\lambda ,n,k),$ waarin $\lambda$ de partitie is, bijvoorbeeld [5,4,2,2], $n$ het totaal aantal vakjes en $k$ het maximaal aantal getallen in het tableau. $k$ is ten minste gelijk aan het aantal rijen in het tableau en ten hoogste gelijk aan $n.$ Het aantal verschillende manieren om zo een semistandaard young-tableau maken met de getallen $1,\ldots ,k$ bepaalt men als volgt:

1. Bepaal voor elk vakje in het tableau de "hoeklengte" (Engels: hook length), dit is het aantal vakjes rechts van het vakje in dezelfde rij, plus het aantal vakjes onder het vakje in dezelfde kolom, plus 1. Vermenigvuldig de hoeklengtes van alle vakjes.
2. Schrijf in elk vakje in het tableau het getal $k+j-i,$ waarin $i$ het volgnummer van de rij is en $j$ het volgnummer van de kolom; de nummering begint linksboven bij nul. Vermenigvuldig al deze getallen.
3. Deel het product uit stap 2 door het product uit stap 1. Dit is het aantal mogelijke semistandaard young-tableaus.

Voorbeeld: bepaal het aantal semistandaard young-tableaus ([2,1], 3, 3), dus van de vorm

[ ][ ]
[ ]

1. de hoeklengten zijn:

[3][1]
[1]

2. de getallen $k+j-i$ zijn:

[3][4]
[2]

3. het aantal is dus: (3.4.2)/(3.1.1) = 8. Er zijn inderdaad acht verschillende geldige opvullingen mogelijk:

[1][1]  [1][1]  [1][2]  [1][2]  [1][3]  [1][3]  [2][2]  [2][3]  
[2]     [3]     [2]     [3]     [2]     [3]     [3]     [3]     

Dit is de verzameling SSYT([2,1], 3, 2). De standaard young-tableaus van de vorm [2,1] vormen daar een deelverzameling van, namelijk:

[1][2]  [1][3]  
[3]     [2]     

Naast deze twee zijn er nog twee andere standaard young-tableaus met drie vakjes:

[1]  en  [1][2][3]
[2]
[3]

Het aantal standaard young-tableaus met $n=0,1,2,3,\ldots$ vakjes wordt gegeven door de reeks:

1, 1, 2, 4, 10, 26, 76, 232, 764, 2620, 9496, ... (rij A000085 in OEIS).

Tralie van Young

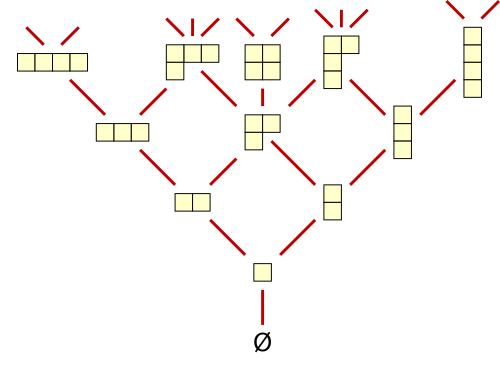
De Tralie van Young is een partieel geordende verzameling en een tralie die bestaat uit alle gehele partities. Ze bevat alle young-diagrammen met 0,1, 2, 3, ... vakjes en kan voorgesteld worden in een hasse-diagram:

De rijen in dit diagram geven alle mogelijke partities aan van verzamelingen met $n=0,1,2,3,\ldots$ elementen. Het aantal diagrammen (partities) op elke rij is de waarde van de partitiefunctie $p(n):p(1)=2,\ p(2)=2,\ p(3)=3,\ p(4)=5,\ldots$

De verbindingen geven aan welke young-diagrammen kunnen bekomen worden door één vakje aan een young-diagram toe te voegen of er één vakje uit weg te nemen.

Een young-diagram met $n$ vakjes kan op de volgende manieren uitgebreid worden naar een diagram met $n+1$ vakjes:

• voeg een vakje toe aan de bovenste lijn
• voeg een vakje toe aan een lijn die korter is dan de lijn erboven
• voeg onderaan een nieuwe lijn toe met één vakje.

Een young-diagram met $n$ vakjes kan op de volgende manieren verkleind worden naar een diagram met $n-1$ vakjes:

• verwijder het meest rechtse vakje in de onderste lijn (als er slechts één vakje in die lijn staat verdwijnt ze uit het diagram)
• verwijder het meest rechtse vakje in een lijn die langer is dan de lijn eronder.

Zie ook

• Jeu de taquin

Bronnen, noten en/of referenties