Elektriciteitswetten van Kirchhoff

De elektriciteitswetten van Kirchhoff zijn twee wetten in de elektriciteitsleer die uitspraken doen over de stromen en spanningen in een elektrisch netwerk. De wetten stellen dat in een knooppunt geen stroom kan verdwijnen en zijn erop gebaseerd dat tussen twee knooppunten in een circuit de wet van Ohm of een uitbreiding daarvan van toepassing is. De wetten zijn genoemd naar de natuurkundige Gustav Robert Kirchhoff. Ze werden voor het eerst in 1845 beschreven en kunnen worden afgeleid uit de wetten van Maxwell. De wetten van Kirchhoff spelen een belangrijke rol in de elektrotechniek, vooral in de netwerkanalyse.
De Franse natuurkundige Claude Pouillet 1791-1868 deed onderzoek naar elektrische verschijnselen en stelde een wet voor een stroomkring op, die een voorloper van de wetten van Kirchhoff was. De stralingswet van Kirchhoff is ook een natuurkundige wet die naar Kirchhoff is genoemd, maar heeft betrekking op een ander vakgebied binnen de natuurkunde, op thermodynamica.
De eerste wet van Kirchhoff[bewerken | brontekst bewerken]
Uit het principe van behoud van elektrische lading volgt de eerste wet van Kirchhoff, ook wel de stroomwet van Kirchhoff genoemd. De wet luidt:
In elk knooppunt van een elektrisch netwerk is de som van de stromen die in dat punt samenkomen gelijk aan de som van de stromen die vanuit dat punt vertrekken.
Anders geformuleerd: In elk knooppunt van een elektrisch netwerk is de algebraïsche som van de stromen , waarbij ingaande stromen positief en uitgaande negatief worden gerekend, gelijk aan nul:
Het knooppunt kan stroom niet opslaan of afgeven.
De tweede wet van Kirchhoff[bewerken | brontekst bewerken]
Uit het principe van behoud van energie volgt de tweede wet van Kirchhoff, ook wel de spanningswet van Kirchhoff genoemd. De wet luidt:
De som van de elektrische potentiaalverschillen , rekening houdend met de richting, in elke gesloten kring in een netwerk is gelijk aan nul.
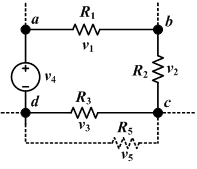
De polariteiten van de potentiaalverschillen in een stroomkring worden bij afspraak bepaald met de tekenconventie. Dit wordt toegelicht aan de hand van de afbeelding van een gesloten stroomkring of lus abcda waarin drie weerstanden , en in serie met een spanningsbron zijn opgenomen. Deze lus mag deel uitmaken van een groter netwerk met bijkomende lussen, zoals met de tweede lus gevormd door en . De tekenconventie houdt het volgende in. Men kiest arbitrair een bepaalde richting bij rondgang in de lus. Als men voor de gekozen richting in de lus gaat van een hogere potentiaal naar een lagere dan is het potentiaalverschil positief te rekenen, als men gaat van een lagere potentiaal naar een hogere dan is het potentiaalverschil negatief. Met deze conventie zijn alle potentiaalverschillen over de weerstanden positief en die over de spanningsbron negatief. Had men voor de andere richting, dus linksom, gekozen dan zijn de potentiaalverschillen over de weerstanden negatief en die over de spanningsbron positief.

De tweede wet van Kirchhoff kan gegeneraliseerd worden voor een willekeurige lus waarin geen veranderlijke magnetische velden optreden. In de weerstanden en de spanningsbronnen moet immers altijd een stationair elektrisch veld heersen. Dit is het veld na voorbijgang van alle overgangsverschijnselen. Dit is het veld dat de ladingsdragers in beweging houdt, de elektronen in vaste stoffen of ionen in een elektrolytoplossing. De arbeid die nodig is om een eenheidslading over dit veld te verplaatsen over een afstand is gelijk aan
Deze arbeid is ook gelijk aan het kleine potentiaalverschil dat tussen twee punten gescheiden door de afstand ontstaat. Immers men heeft steeds en voor een rechte lijn tussen die twee punten wordt dit
Integreren tussen de punten en geeft
Vertrekt men van een punt in een willekeurige lus en maakt men een rondgang in een bepaalde richting om uiteindelijk terug uit te komen bij het punt dan krijgt men
De kringintegraal van de stationaire veldsterkte in een willekeurige lus is dus evenals de kringintegraal van een eventueel elektrisch veld buiten het materiaal van de lus gelijk aan nul. Dit is de algemene en integrale uitdrukking van de tweede wet van Kirchhoff. Daarmee is ook bewezen dat het stationaire elektrische veld conservatief is.
Bibliografie[bewerken | brontekst bewerken]
- R Kronig. Leerboek der Natuurkunde, zesde druk 1962.






















