Eindige-elementenmethode

Voorbeeld van een eindige-elementenberekening. Een thermo-mechanisch probleem: een blokje metaal wordt vooral in het centrum verhit en gekoeld via kleine koelkanaaltjes.
1 Het "maken" (programmeren) van een model,
2 Het rekenprogramma verdeelt het model in kleine elementjes.
3 Na het aanbrengen van thermische belasting en de koeling berekent het programma de temperatuurverdeling in °C) en
4 mechanische spanningen in MPa)
5 De vervorming wordt overdreven weergegeven.

De eindige-elementenmethode (e.e.m.) is een rekenmethode waarmee partiële differentiaalvergelijkingen en integraalvergelijkingen benaderend kunnen worden opgelost. Belangrijke toepassingen hiervan vindt men in de ingenieurswetenschappen, waar men deze methode bijvoorbeeld gebruikt om de sterkte van ingewikkelde constructies en constructie-elementen te berekenen. De methode is ontwikkeld, omdat analytische rekenmethoden onvoldoende mogelijkheden bieden, of te complexe berekeningen vergen. De methode vindt zijn toepassing bij sterkteberekeningen, maar ook bij elektromagnetisme, warmteleer, stromingsleer en nog vele andere disciplines.

Wiskundig kan worden aangetoond dat bij het verkleinen van de elementen, de oplossing die met de e.e.m. wordt bereikt, nadert tot de analytisch juiste oplossing (convergentie). Wel kunnen bij onjuiste modellering fouten worden gemaakt die ernstige gevolgen kunnen hebben.

Toepassingen[bewerken | brontekst bewerken]

De methode wordt met name ingezet in de werktuigbouwkunde, maar vindt ook toepassing in de luchtvaartindustrie, de ruimtevaart, de scheepvaart, de weg- en waterbouwkunde en in de sterkteleer in het algemeen. Met de eindige-elementenmethode kan bijvoorbeeld het gewicht van een constructie worden geoptimaliseerd, hetgeen een groot effect kan hebben op de kosten of de omvang van de constructie.

Er zijn vele types berekening:

lineaire statische sterkteberekeningen (het meest gebruikte type berekening)
Niet-lineaire berekeningen, waarbij ook plastisch gedrag wordt meeberekend
eigenfrequentiebepaling
thermische berekening
knikberekening
schok (tijdafhankelijke berekening)
elektrostatische en -dynamische berekeningen
combinaties van bovengenoemde (multiphysics)

Werking van de methode[bewerken | brontekst bewerken]

In de eindige-elementenmethode deelt degene die de berekeningen doet, een constructie op in een (eindig) aantal elementen, en koppelt deze elementen aan elkaar door middel van knooppunten (nodes). Aan deze koppelingen wordt, afhankelijk van het soort element, een aantal eisen (randvoorwaarden) gesteld. In elk geval moeten de nodes van de elementen zich tegelijk met elkaar verplaatsen, want anders zou er een gat in de constructie ontstaan. Het bepalen van de knooppunten en koppelingen komt overeen met het bepalen van een rooster.

Door deze methodiek is het mogelijk het gedrag van een complexe constructie te benaderen door middel van een matrixvergelijking.

In het geval van een lineair statische berekening is de matrixvergelijking:

[K]\{u\}=\{F\}

Daarbij is $[K]$ de stijfheidsmatrix voor het gehele systeem, $\{u\}$ de verplaatsingen van de knooppunten in de afzonderlijke richtingen en $\{F\}$ de belastingen (krachten / momenten) op de knooppunten in alle richtingen.

Het doel is de verplaatsingsvector $\{u\}$ te bepalen, en daaruit de spanningen en rekken, waaruit dan de sterkte van de constructie bij belasting $\{F\}$ volgt.

Om een nauwkeurige berekening te doen, moeten de elementen voldoende klein gekozen worden. Daardoor worden de rekenmodellen over het algemeen wel groot.

Types elementen[bewerken | brontekst bewerken]

De elementen die gebruikt worden in deze methoden, zijn, al naargelang het aantal dimensies (D):

(1D) Staafelementen
(2D) Oppervlakte-elementen (driehoekig of met vier hoekpunten)
(3D) Volume-elementen (tetraëder of kubus)

Elk element krijgt op basis van de getekende geometrie, de (niet getekende) geometrische parameters als plaatdikte, doorsnede, en het gebruikte materiaal, de stijfheidseigenschappen toegewezen. Bij het uitvoeren van een dynamische berekening is het nodig ook massaeigenschappen toe te wijzen of zelfs de demping, in het geval van gedwongen trillingen. Bij een thermische berekening moeten uiteraard de thermische eigenschappen worden toegewezen.

In het algemeen bieden 2D-elementen (2D-modellen) grote voordelen vanwege de korte rekentijd. Dan dienen echter geometrie, randvoorwaarden en belastingen tweedimensionaal te zijn. Het probleem mag zowel prismatisch als axiaalsymmetrisch zijn.

Er wordt verder onderscheid gemaakt tussen zogenaamde H-elementen en P-elementen:

H-elementen hebben een vaste instelling voor de verplaatsingsfunctie (bijv 1e-, 2e-, 3e-orde polynoom), door de gebruiker ingesteld. Hogere rekennauwkeurigheid wordt verkregen door fijnere mazen, d.w.z. kleinere elementen, te genereren.
De P-methode heeft een variabele polynoom en kent complexere elementvormen. Hogere nauwkeurigheid wordt bereikt door de graad van de polynoom te vergroten.

Het meest toegepast wordt de H-methode om historische reden. De P-methode is gebruiksvriendelijker, maar vroeger had men nog niet de rekenkracht om deze methode tot standaard te maken.

Geschiedenis[bewerken | brontekst bewerken]

De methodiek is ontstaan omstreeks 1940, al voordat computers bestonden. Sinds de intrede van de PC heeft de eindige-elementenmethode (In het Engels: "Finite Element Method" (FEM) / of "Finite Element Analysis") een grote vlucht genomen. En ook ontwikkelingen in de ruimtevaart hebben de eindige-elementenmethode een boost gegeven. In de ruimtevaart was de nood hoog om vooraf al globaal te bepalen of een constructie zou voldoen aan de sterkte- en stijfheidseisen. Het eerste grote eindige-elementenpakket was dan ook NASTRAN (NAsa STRuctural ANalysis). Ook de koppeling aan een 3D computer-aided design (CAD) pakket biedt grote voordelen: het moeizame opbouwen van geometrie is niet meer nodig, waardoor snel de invloed van ontwerpwijzigingen op de resultaten (spanningen / resonantiefrequenties / temperaturen / verplaatsingen / doorbuiging) kan worden bepaald. Dit noemt men isogeometrische analyse.

Problemen[bewerken | brontekst bewerken]

Vooral een juiste bepaling van de belasting die op de structuur of het onderdeel inwerkt, is cruciaal voor de betrouwbaarheid van een berekening. Daarbij worden wel benaderingen gemaakt, bijvoorbeeld bij aannames over de maximale:

windkracht op een hoog gebouw
kracht van een aardbeving
belasting van een brug door personen, trein of ander zwaar voertuig
krachten op een vliegtuigvleugel in omstandigheden zoals onweer.

De nacontrole (post-processing) is evenzeer van cruciaal belang. Dit is het proces waarin de gebruiker de eindige-elementenmethode-berekening controleert op een aantal cruciale punten. Zo moeten bijvoorbeeld de gevonden reactiekrachten gelijk zijn aan de totaal aangebrachte belasting. Ook het handmatig op enkele punten controleren van de berekende spanningen behoort standaard tot de controles. Ook moet gecontroleerd worden of onvolkomenheden van de software/elementen de berekening beïnvloed hebben. De elementverdeling kan b.v. te grof zijn om een goede indicatie van spanningsconcentraties te krijgen.

Voorbeeld[bewerken | brontekst bewerken]

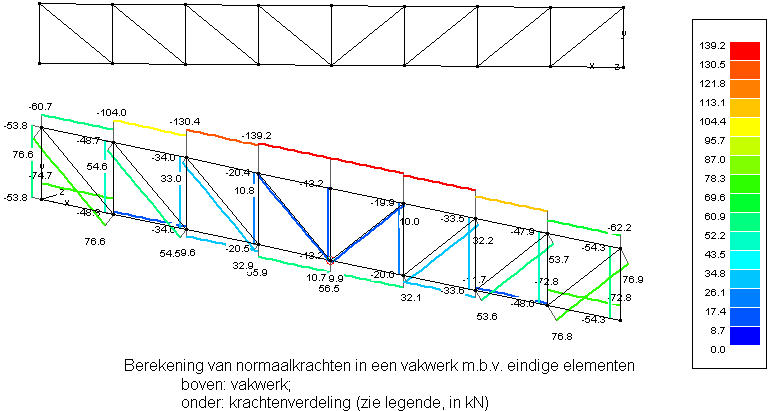
In het onderstaande voorbeeld werden de normaalkrachten in een constructie bepaald. De elementen bestaan uit lijnvormige delen in een vakwerk-constructie, zoals die wel in hijskranen wordt toegepast.

Software[bewerken | brontekst bewerken]

Voor de berekeningen is specifieke software nodig. Er bestaan vele commerciële- en ook enkele open source pakketten.

Software	Toepassing	Ontwikkelaar	Versie	Gestart	Licentie	Commercieel Vrij gebruik Studentenversie	Platform
Agros2D	Multiplatform open-source-applicatie voor oplossingen van fysische problemen gebaseerd op de Herms-bibliotheek.	University of West Bohemia	3.2	2014-03-03	GNU GPL	Vrij	Linux, Windows
CalculiX	Dit is een Open Source FEA project. De "solver" gebruik gedeeltelijk compatibele ABAQUS bestandsformaat. De pre/post-processor genereert inputdata voor veel FEA- en CFD-applicaties.	Guido Dhondt, Klaus Wittig	2.16	2019-11-24	GNU GPL	Vrij	Linux, Windows
DIANA FEA	Algemeen bruikbaar eindig-elementenpakket voor civiele, structurele en geotechnische engineering.	DIANA FEA BV, (Nederland)	10.1	2016-11-14	Proprietary commercial software	commercieel	Windows, Linux
deal.II	Bevat een set tools voor eindige-elementenberekeningen op laptops tot geclusterde servers. Geschreven in C++	Wolfgang Bangerth, Timo Heister, Guido Kanschat, Matthias Maier et al.	9.0	2018-05-12	LGPL	Vrij	Linux, Unix, Mac OS X, Windows
DUNE	Distributed Unified Numerics Environment, Geschreven in C++	DUNE Developer team	2.4.1	2016-02-29	GPL Version 2 with Run-Time Exception	Vrij	Linux, Unix, Mac OS X
Elmer	Open source multi-fysische simulatiesoftware ontwikkeld door het Finse ministerie van educatie CSC. Hoofdzakelijk geschreven in Fortran, C en C++	CSC	8.2	2016-03-15	GPL	Vrij	Linux, Mac OS X, Windows
FEBio	Eindige elementen voor biomechanica.	University of Utah (MRL), Columbia University (MBL)	2.7	April, 2018	Custom	Vrij	Linux, Mac OS X, Windows
FEniCS Project	Software pakket ontwikkeld met het doel om geautomatiseerd differentiaalvergelijkingen op te lossen.	FEniCS Team	1.6.0	2015-07-29	LGPL (Core) & GPL/LGPL (Non-Core)^[1]	Vrij	Linux, Unix, Mac OS X, Windows
FEATool Multiphysics	MATLAB Multi fysische-simulatietoolbox voor eindige-elementenmethode.	Precise Simulation	1.10	2019-05-17	Proprietary EULA	Vrij voor persoonlijk gebruik^[2]	Windows, Mac OS X, Linux, Unix
FreeFEM^[3]	Vrij eindige-elementenpakket met eindige-elementenanalyse-software voor multifysische symulaties. Geschreven in C++.	Sorbonne University^[4] and Jacques-Louis Lions Laboratory^[5]	4.2.1	2019-06-06	LGPL	Vrij	Linux, MacOS, Windows, Solaris
GOMA	GOMA is een open source eindige-elementenpakket met eindige-elementenanalyse-software voor multifysische simulaties. Van oorsprong gebaseerd op roterende geometrie.	Sandia National Laboratories, University of New Mexico	6.1	Aug 28, 2015	GPL Version 2	Vrij	Linux
GetFEM++	Een algemene eindige-elementen-bibliotheek geschreven in C++ met interfaces voor Python, Matlab en Scilab.	Yves Renard, Julien Pommier	5.0	2015-07	LGPL	Vrij	Unix, Mac OS X, Windows
Hermes Project	Een modulaire C/C++-bibliotheek voor snelle ontwikkeling van tijdafhankelijke problemen.	hp-FEM group	3.0	2014-03-01	LGPL	Vrij	Linux, Unix, Mac OS X, Windows
Mathematica^[6]	General purpose computation software.	Wolfram Research		Regularly	Proprietary		Linux, Mac OS X, Windows, Raspbian, Online service.
MATLAB	MATLAB Toolbox for solving structural, thermal, electromagnetics, and other general PDEs	MathWorks	3.3 (R2019b)	2019-09-11	Proprietary commercial software	Commercieel	Linux, Mac OS X, Windows
MOOSE	Objectgeoriënteerde eindige-elementenvakwerk-berekeningen geschreven in C++.	Idaho National Laboratory		regularly	LGPL	Vrij	Unix, Mac OS X
OOFEM	Objectgeoriënteerde eindige-elementensolver geschreven in C++.	Bořek Patzák	2.4	2016-02-15	GPL Version 2	Vrij	Unix, Windows
OpenSees	Software voor aardbevingsberekeningen aan constructies.				Non Commercial	Vrij	Unix, Linux, Windows
SESAM (FEM)	Software voor sterkte en hydrodynamische analyses van schepen en offshoreconstructies.	DNV GL		regularly	Proprietary, SaaS		Windows, Web browser
Range Software	Multifysische eindige-elementenberekeningen.	Tomáš Šoltys	3.0	2018-04-30	GPL	Vrij	Linux, Windows
Z88/Z88Aurora	Gratis te gebruiken eindige-elementenpakket Z88Aurora V4, voor lineaire en niet lineaire analyses, frequentie- en thermische analyses.	Frank Rieg	Z88 V15, Z88Aurora V5	2017-07-17, 2019-04-01	GNU GPL, Custom	Vrij	Linux, Windows, Mac OS X
Abaqus	Geavanceerde software van SIMULIA, eigendom van Dassault Systemes	Abaqus Inc.	2019	2019-12	Proprietary commercial software	Commercieel	Linux, Windows
CONSELF	CAE pakket voor de browser.	CONSELF SRL	2.9	2015-10	SaaS		Web browser
FreeCAD	Parametrische driedimensionale modelleer- en rekenpakket. Ook geschikt om externe solvers te gebruiken zoals Calculix, Z88, Elmer en OpenFoam.	FreeCAD Team	0.18	2019-03-12	LGPL 2	Vrij	Linux, Windows, Mac OS X
ADINA	Eindige-elementensoftware voor berekenen van constructies, vloeistof- en warmtestromen en magnetische velden.	Adina R&D			Proprietary commercial software	Commercieel
Advance Design	Software voor eindige-elementenanalyses, inclusief check volgens internationale ontwerp eurocodes	GRAITEC	2014	2013-09	Proprietary commercial software	Commercieel
Autodesk Simulation	Eindige-elementensoftware van Autodesk.	Autodesk			Proprietary commercial software	Commercieel	Windows
ANSYS	In Amerika ontwikkeld en gemaakt, volledig CAE-softwarepakket.	Ansys Inc.	19.2	2018-09-18	Proprietary commercial software	Commercieel en studentenversie voor 32.000 nodes/elements^[7]	Windows, Linux
COMSOL Multiphysics	Multifysische eindige-elementenanalyse. (voorheen FEMLAB)	COMSOL Inc.	5.5	2019-11-14	Proprietary EULA		Linux, Mac OS X, Windows, Web browser
CosmosWorks	onderdeel van SolidWorks	Dassault Systèmes SolidWorks Corp.			Proprietary commercial software	Commercieel	Windows
Quickfield	Eindige0elementenmethode voor thermische en spanningsanalyses.	Tera Analysis Ltd	6.4 ^[8]	2020-04-17	Proprietary EULA	Commerciele en studentenversie^[9]	Windows
Pam Crash	Vooral te gebruiken voor dynamische en botsingsanalyses.	ESI	15.5.1	2020-03-05	Proprietary commercial software	Commercieel	Linux, Windows
LS-DYNA	Vooral te gebruiken voor dynamische en botsingsanalyses.	LSTC - Livermore Software Technology Corporation	R8.0	2015-03	Proprietary commercial software	Commercieel	Linux, Windows
Nastran	Door NASA ontwikkeld en commercieel verkrijgbaar bij verschillende bedrijven.	MSC NASTRAN, Siemens PLM NX Nastran^[10]	2014	2014	Proprietary EULA	Commercieel	Linux, Mac OS X, Windows
RFEM	Driedimensionale eindige-elementenanalyse-software.	Dlubal Software	5.06	2016-02	Proprietary commercial software	Commerciele en studentenversie^[11]	Windows
SimScale	Duits 100% web-based CAE platform	SimScale GmbH	14	2013-07	SaaS	Heeft ook een studentenversie^[12]	Web browser
VisualFEA	Eindige-elementenanalyse-software voor structurele en termische belastingen.	Intuition Software	5.11	2016-01	Proprietary software	Commerciele en studentenversie beschikbaar^[13]	Mac OS X, Windows
JCMsuite	Eindige-elementenanalyse-software voor structurele, termische en elektromagnetische golven.	JCMwave GmbH	3.6.1	2017-01-27	Proprietary EULA		Linux, Windows
JMAG	Twee- en driedimensionale eindige-elementenanalyse-software voor structurele, termische en elektromagnetische velden.	JSOL	18.1	2019-06	Proprietary commercial software	Commercieel en studentenversie	Linux, Windows, Web browser
StressCheck	Eindige-elementenanalyse-software gebaseerd op hp-FEM, vooral met volume-elementen.	ESRD, Inc.	10.5	2019-06-06	Proprietary commercial software	Commercieel	Windows
SDC Verifier	Een uitbreiding van Ansys en Femap en Simcenter voor vermoeiing- knik- en bucklingberekeningen volgens internationale codes.	SDC Verifier	5.3.1	2020-03	Proprietary commercial software	Commercieel en studentenversie	Windows

Bronnen, noten en/of referenties

↑ FEniCS Project. Geraadpleegd op 21 juni 2017.
↑ FEATool Multiphysics - Product Information. Geraadpleegd op 12 juni 2018.
↑ (en) FreeFem++. freefem.org. Geraadpleegd op 30 november 2018.
↑ (en) Sorbonne Université | Lettres, Médecine, Sciences. www.sorbonne-universite.fr. Geraadpleegd op 30 november 2018.
↑ (en) Curie, UPMC - Université Pierre et Marie, Jacques-Louis Lions Laboratory (LJLL) - UMR 7598 - SCIENCE. sciences.sorbonne-universite.fr. Gearchiveerd op 1 december 2018. Geraadpleegd op 30 november 2018.
↑ Mathematica Documentation
↑ Student Products - Free Simulation Software. Ansys.com. Geraadpleegd op 28 mei 2017.
↑ http://quickfield.com/allnews/qf64.htm
↑ http://www.quickfield.com/free_soft.htm
↑ NX Nastran: Siemens PLM Software. Plm.automation.siemens.com. Geraadpleegd op 28 mei 2017.
↑ Free Student License | Dlubal Software. Dlubal.com. Geraadpleegd op 28 mei 2017.
↑ Plans & Pricing - SimScale Simulation Platform. Simscale.com. Geraadpleegd op 28 mei 2017.
↑ Browsing VisualFEA (Finite Element Analysis) by Title. Ecommons.cornell.edu (1 maart 2016). Geraadpleegd op 28 mei 2017.

[1] FEniCS Project. Geraadpleegd op 21 juni 2017.

[2] FEATool Multiphysics - Product Information. Geraadpleegd op 12 juni 2018.

[3] (en) FreeFem++. freefem.org. Geraadpleegd op 30 november 2018.

[4] (en) Sorbonne Université | Lettres, Médecine, Sciences. www.sorbonne-universite.fr. Geraadpleegd op 30 november 2018.

[5] (en) Curie, UPMC - Université Pierre et Marie, Jacques-Louis Lions Laboratory (LJLL) - UMR 7598 - SCIENCE. sciences.sorbonne-universite.fr. Gearchiveerd op 1 december 2018. Geraadpleegd op 30 november 2018.

[6] Mathematica Documentation

[7] Student Products - Free Simulation Software. Ansys.com. Geraadpleegd op 28 mei 2017.

[8] ttp://quickfield.com/allnews/qf64.htm

[9] ttp://www.quickfield.com/free_soft.htm

[10] NX Nastran: Siemens PLM Software. Plm.automation.siemens.com. Geraadpleegd op 28 mei 2017.

[11] Free Student License | Dlubal Software. Dlubal.com. Geraadpleegd op 28 mei 2017.

[12] Plans & Pricing - SimScale Simulation Platform. Simscale.com. Geraadpleegd op 28 mei 2017.

[13] Browsing VisualFEA (Finite Element Analysis) by Title. Ecommons.cornell.edu (1 maart 2016). Geraadpleegd op 28 mei 2017.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]