Stelling van Descartes
In de meetkunde is de stelling van Descartes een vergelijking tussen de straal van vier onderling rakende cirkels. De stelling geeft aan hoe uitgaande van drie onderling rakende cirkels een vierde cirkel is te construeren, die aan deze drie raakt. Het is een bijzonder geval van het raakprobleem van Apollonius.
De stelling is naar René Descartes 1596-1650 genoemd. Descartes werd in Frankrijk geboren, maar leefde 20 jaar, van 1628 tot 1649 in de Republiek der Zeven Verenigde Nederlanden. Hij besprak het probleem in 1643 beknopt in een correspondentie met prinses Elizabeth Stuart. Hij gaf in essentie dezelfde oplossing als bij vergelijking (1), waardoor het theorema zijn naam kreeg. Frederick Soddy schreef er in 1936 in Nature een gedicht over.
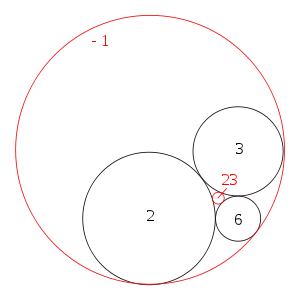
Gegeven drie elkaar rakende cirkels, in de figuur zwart, dan zijn er in het algemeen twee andere cirkels, rood, die als vierde aan de drie eerste cirkels raken. De getallen zijn de krommingen en de stelling van Descartes legt een verband tussen deze krommingen. De twee mogelijke cirkels bij de drie andere die elkaar raken worden de cirkels van Soddy genoemd.
Definitie van kromming[bewerken | brontekst bewerken]
De stelling van Descartes wordt in het algemeen geformuleerd met het begrip kromming van de cirkel. Deze kromming is gedefinieerd als , waarin de straal is. Hoe groter de cirkel, hoe kleiner de kromming en vice versa.
Het plusteken in slaat op een cirkel die aan zijn buitenkant raakt aan de andere cirkels, zoals de zwarte cirkels in de afbeelding. Voor een cirkel die de andere cirkels aan zijn binnenkant raakt wordt het minteken gebruikt.
Een lijn kan in de stelling van Descartes als een ontaarde cirkel worden gezien, met kromming .
Stelling[bewerken | brontekst bewerken]
Als vier elkaar onderling rakende cirkels krommingen hebben, met , dan is volgens de stelling van Descartes:
Om de straal te vinden van een vierde cirkel die raakt aan drie gegeven cirkels, kan de vergelijking het best worden herschreven als:
Het ± teken laat zien dat er in het algemeen twee oplossingen voor zijn. Daar zijn twee uitzonderingen op:
- Als twee van de drie cirkels ontaard zijn, valt samen met de enige niet-ontaarde cirkel en
- in het 'pathologische' geval dat , en alle drie ontaard zijn, is ook ontaard.













