Kromming (meetkunde)

In de meetkunde, een deelgebied van de wiskunde, wordt de term kromming gebruikt voor een aantal losjes aan elkaar gerelateerde concepten die in verschillende deelgebieden van de meetkunde worden gebruikt. Intuïtief gesproken is kromming de mate waarin een meetkundig object afwijkt van platheid of, in het geval van een lijn, van rechtheid, maar dit wordt afhankelijk van de context op verschillende manieren gedefinieerd. Er bestaat een belangrijk onderscheid tussen extrinsieke kromming, wat voor objecten die zijn ingebed in een andere ruimte (meestal een euclidische ruimte) op een manier wordt gedefinieerd die verband houdt met de kromtestraal van cirkels die raken aan het object, en intrinsieke kromming, die op elk punt in een differentiaalvariëteit is gedefinieerd.

Het oervoorbeeld van extrinsieke kromming is dat van een cirkel, die een kromming heeft die overal gelijk is aan de inverse van haar straal. Kleinere cirkels hebben scherpere bochten en dus een grotere kromming. De kromming van een gladde kromme wordt op elk punt gedefinieerd als de kromming van haar kromtestraal.

In een vlak, dat wil zeggen een scalaire kwantiteit, maar dan in drie of meer dimensies, wordt het vlak beschreven door een krommingsvector, die niet alleen rekening houdt met de richting van de kromming, maar ook met de scherpte van de bocht. De kromming van meer complexe objecten, zoals oppervlakken of zelfs gekromde $n$-dimensionale ruimten, wordt beschreven door meer complexe objecten uit de lineaire algebra, zoals de algemene krommingstensor van Riemann.

Kromming van vlakke krommen

float

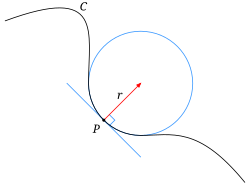
Laat $C$ een vlakke kromme zijn. De kromming van $C$ in een punt $P$ van $C$ is een maat voor de grootte van de richtingsverandering van een raaklijn aan $C$ door $P$, als $P$ naar de andere dichtbijzijnde punten wordt verplaatst. Er zijn een aantal gelijkwaardige manieren waarop dit idee kan worden gepreciseerd.

Een manier is meetkundig. Het is natuurlijk om de kromming van een lijn gelijk aan nul te stellen. De kromming van een cirkel met straal $R$ is groot als de straal klein is en klein als de straal groot is. De kromming $\kappa$ van een cirkel is daarom gedefinieerd als de omgekeerde van de straal:

$\kappa ={\frac {1}{R}}$.

Bij een willekeurige kromme $C$ en een punt $P$ op deze kromme bestaat er een unieke cirkel of lijn die de kromme in de buurt van $P$ het dichtst mogelijk benadert: de zogeheten osculerende cirkel in $P$. De kromming van $C$ in $P$ wordt dan gedefinieerd als de kromming van deze osculerende cirkel of lijn. De straal van de kromming is bijgevolg de reciproque van de kromming.

Een andere manier om de kromming te begrijpen is natuurkundig. Stel dat een deeltje zich langs de kromme voortbeweegt met snelheid $\mathbf {v}$, met $|\mathbf {v} |=1$. Als men de tijd $t$ als parameter neemt voor de plaats van $P$ op $C$ biedt dit een natuurlijke parametrisatie voor de kromme. De richting van de raakvector $\mathbf {T}$, waarvoor $|\mathbf {T} |=1$, hangt van de tijd af. De kromming is dan de grootte van de mate van verandering van $\mathbf {T}$.

$\kappa =\left|{\frac {\mathrm {d} \mathbf {T} }{\mathrm {d} t}}\right|$

De kromming $\kappa$ is hierin gelijk aan de middelpuntzoekende versnelling, die het deeltje de kromming van $C$ in $P$ doet doorlopen.

Het is aan te tonen dat deze middelpuntzoekende versnelling voor een afstand die in de limiet naar nul gaat, gelijk is aan de eerder gedefinieerde kromming $\kappa$.

Definitie

De vectoren $\mathbf {T}$ en $\mathbf {N}$ in twee punten op een vlakkromme, een getransleerde versie van het tweede frame, de stippellijn, en de verandering $\delta (\mathbf {T} )$ in $\mathbf {T}$. $\delta s$ is de afstand tussen de punten. In de limiet zal ${\tfrac {\mathrm {d} \mathbf {\mathbf {T} } }{\mathrm {d} t}}$ in de richting van $N$ gaan en beschrijft de kromming de snelheid van de rotatie van het frame.

De kromme $C$ heeft de parameterweergave $\theta (t)=(x(t),y(t))$ zo gekozen dat over het gehele domein

$|\ \theta '\ |^{2}=x'(t)^{2}+y'(t)^{2}\neq 0$.

Wanneer naar de kromming van $C$ in een punt $P$ wordt gekeken, kan voor $C$ een equivalente parameterweergave $\gamma$ worden gekozen, zodat

$|\ \gamma '\ |^{2}=x'(t)^{2}+y'(t)^{2}=1$.

Het is een voorwaarde dat dit tenminste in $P$ geldt.

Kies $\mathbf {T} (t)$ en $\mathbf {N} (t)$ zodat $|\mathbf {T} (t)|=1$ en $|\mathbf {N} (t)|=1$.

$\mathbf {T} (t)$, de kromming $\kappa (t)$ en de kromtestraal $R(t)$ worden gegeven door

$\mathbf {T} (t)=\gamma '(t)$,

$\mathbf {T} '(t)=\kappa (t)\mathbf {N} (t)$,

$\kappa (t)=|\mathbf {T} '(t)|=|\gamma ''(t)|=\left|k(t)\right|$ en

$R(t)={\frac {1}{\kappa (t)}}$.

Er wordt hier naar de parameter $t$ gedifferentieerd.

Teken van de kromming

Het teken van de getekende kromming $k$ geeft de richting aan, waarin de eenheidsraakvector roteert als een functie van de parameter langs de kromme. Als de eenheidsraaklijn tegen de klok in draait, dan geldt dat $k>0.$ Als deze met de klok meedraait, geldt $k<0.$

De getekende kromming hangt af van de betreffende parametrisatie, die voor deze kromme is gekozen. De eenheidscirkel kan bijvoorbeeld worden geparametriseerd door $(\cos(\theta ),\sin(\theta ))$ (tegen de klok in, met $k>0$), of door $(\cos(-\theta ),\sin(-\theta ))$ (met de klok mee, met $k<0$). Preciezer geformuleerd hangt de ondertekende kromming alleen af van de keuze van oriëntatie van een ondergedompelde kromme. Elke ondergedompelde kromme in het vlak laat twee mogelijke oriëntaties toe.

Lokale uitdrukkingen

Voor een vlakke kromme die in cartesische coördinaten parametrisch wordt gegeven door $\gamma (t)=(x(t),y(t)),$ is de kromming

$\kappa ={\frac {|x'y''-y'x''|}{(x'^{2}+y'^{2})^{3/2}}},$

waar accenten verwijzen naar afgeleiden met betrekking tot de parameter $t.$ De getekende kromming $k$ is

$k={\frac {x'y''-y'x''}{(x'^{2}+y'^{2})^{3/2}}}.$

Deze kan op een coördinaat-onafhankelijke wijze worden uitgedrukt als

$k={\frac {\det(\gamma ',\gamma '')}{\|\gamma '\|^{3}}},\quad \kappa ={\frac {|\det(\gamma ',\gamma '')|}{\|\gamma '\|^{3}}}.$

Kromming van een grafiek

Voor het minder algemene geval van een vlakkromme die expliciet wordt gegeven als $y=f(x),$ en door nu accenten te gebruiken om de afgeleiden met betrekking tot de $x$-coördinaat weer te geven, is de kromming

$\kappa ={\frac {|y''|}{(1+y'^{2})^{3/2}}}$ ,

en is de getekende kromming

$k={\frac {y''}{(1+y'^{2})^{3/2}}}$

Deze uitdrukkingen zijn eveneens geldig voor impliciete functies $f(x,y)=0,$ waar de afgeleiden eveneens kunnen berekend worden.

Deze vergelijking komt veel voor in de natuurkunde en de techniek; bijvoorbeeld in de vergelijkingen van buiging in balken, de 1D trilling van een gespannen snaar, benaderingen van vloeistofstromen rond oppervlakken (in de luchtvaart), en de vrij oppervlak randvoorwaarden in oceaangolven. In dergelijke toepassingen wordt bijna altijd de aanname gemaakt dat de helling klein is in vergelijking met eenheid, zodat de benadering

$\kappa \approx \left|{\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}\right|$

kan worden gebruikt. Deze benadering levert een relatief eenvoudige lineaire vergelijking op die het verschijnsel beschrijft, dat anders onhandelbaar zou blijven.

Als een kromme in poolcoördinaten wordt gedefinieerd als $r(\theta )$, dan is haar kromming gelijk aan

$\kappa (\theta )={\frac {|r^{2}+2r'^{2}-rr''|}{\left(r^{2}+r'^{2}\right)^{3/2}}}$

waar het accent nu verwijst naar de differentiatie met betrekking tot $\theta$.

Voorbeeld

Beschouw de parabool $y=x^{2}.$ Men kan de kromme relatief eenvoudig parametriseren als $\gamma (t)=(t,t^{2})=(x,y).$ Als men punten gebruikt om de afgeleiden met betrekking tot de parameter $t$ aan te geven, dan geldt

${\dot {x}}=1,\quad {\ddot {x}}=0,\quad {\dot {y}}=2t,\quad {\ddot {y}}=2.$

Substitueer deze waarden en laat de onnodige absolute waarden vallen, dan verkrijgt men

$\kappa (t)=\left|{\frac {{\dot {x}}{\ddot {y}}-{\dot {y}}{\ddot {x}}}{({{\dot {x}}^{2}+{\dot {y}}^{2}})^{3/2}}}\right|={1\cdot 2-(2t)(0) \over (1+(2t)^{2})^{3/2}}={2 \over (1+4t^{2})^{3/2}}$

Kromming van de ruimtekrommen

Zoals ook in het geval van krommen in twee dimensies, is de kromming van een regelmatige ruimtekromme $C$ in drie dimensies (en hoger) de grootte van de versnelling van een deeltje, dat zich met de eenheidssnelheid langs een kromme beweegt. Dus als $\gamma (s)$ de booglengte parametrisatie van $C$ is, dan wordt de eenheidsraakvector $\mathbf {T} (s)$ gegeven door

$\mathbf {T} (s)=\gamma '(s)$

en is de kromming de grootte van de versnelling:

$\kappa (s)=\|\mathbf {T} '(s)\|=\|\gamma ''(s)\|$

De richting van de versnelling is de eenheidsnormaalvector $\mathbf {N} (s),$ die wordt gedefinieerd door

$\mathbf {N} (s)={\frac {\mathbf {T} '(s)}{\|\mathbf {T} '(s)\|}}$

Het vlak met de twee vectoren $\mathbf {T} (s)$ en $\mathbf {N} (s)$ wordt het osculerende vlak op de kromme op $\gamma (s)$ genoemd. De kromming heeft de volgende meetkundige interpretatie. Er bestaat een cirkel in het osculerende vlak die raakt aan $\gamma (s),$ waarvan de Taylor-reeks van de tweede orde op het punt van contact overeenkomt met die van $\gamma (s).$ Dit is de osculerende cirkel op de kromme. De straal van de cirkel $R(s)$ wordt de kromtestraal genoemd, en de kromming is de reciproke van de kromtestraal:

$\kappa (s)={\frac {1}{R(s)}}$

Het raakvlak, de kromming en de normaalvector beschrijven samen het tweede-ordegedrag van een kromme in de buurt van een punt. In drie dimensies wordt het derde-ordegedrag van een kromme beschreven door een daaraan gerelateerde notie van torsie, die de mate meet, waarin een kromme de neiging heeft om een kurkentrekker in de ruimte uit te voeren. De torsie en de kromming worden aan elkaar gerelateerd door de formules van Frenet-Serret (in drie dimensies) en hun generalisaties, in hogere dimensies.

Lokale uitdrukkingen

Voor een parametrisch gedefinieerde ruimtekromme in cartesische coördinaten in drie dimensies gegeven door $\gamma (t)=(x(t),y(t),z(t))$, is de kromming

$\kappa ={\frac {\sqrt {(z''y'-y''z')^{2}+(x''z'-z''x')^{2}+(y''x'-x''y')^{2}\ }}{(x'^{2}+y'^{2}+z'^{2})^{3/2}}}$

waar het accent staat voor differentiatie met betrekking tot de tijd $t.$ Dit kan onafhankelijk van het gebruikte coördinatensysteem worden uitgedrukt door middel van de formule

$\kappa ={\frac {|\gamma '\times \gamma ''|}{|\gamma '|^{3}}}$

waar $\times$ het vectorkruisproduct is. Op gelijkwaardige wijze,

$\kappa ={\frac {\sqrt {\det \left((\gamma ',\gamma '')^{T}(\gamma ',\gamma '')\right)\ }}{\|\gamma '\|^{3}}}$

Hier duidt $T$ de getransponeerde matrix aan. Deze laatste formule is ook geldig voor de kromming van de krommen in een Euclidische ruimte van enige dimensie.

Kromming van boog en koordelengte

Gegeven twee punten $P$ en $Q$ op $C,$ laat $s(P,Q)$ de booglengte van het gedeelte van de krommen tussen $P$ en $Q$ zijn en laat $d(P,Q)$ de lengte van het lijnstuk van $P$ naar $Q$ aangeven. De kromming van $C$ op $P$ wordt nu gegeven door de limiet

$\kappa (P)=\lim _{Q\to P}{\sqrt {{\frac {24\left(s(P,Q)-d(P,Q)\right)}{s(P,Q)^{3}}}\ }}$

waar de limiet, die is genomen in $Q$ het punt $P$ benadert op $C.$ Als noemer kan evengoed $d(P,Q)^{3}$ worden genomen. De formule is geldig in alle dimensies. Door verder de limiet onafhankelijk aan weerszijden van $P$ te nemen, is deze definitie van kromming in sommige gevallen ook geschikt voor een singulariteit in $P.$ De formule volgt door deze te verifiëren voor de osculerende cirkel.

Krommen op oppervlakken

Zadeloppervlak met normale vlakken in de richtingen van de hoofdkrommingen

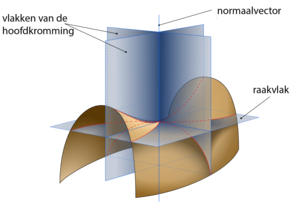
Wanneer een eendimensionale kromme op een tweedimensionaal oppervlak ligt, dat is ingebed in de drie dimensionale $\mathbb {R} ^{3}$, zijn er meer maten van kromming van het oppervlak mogelijk. Dit zijn de normale kromming, de geodetische kromming en geodetische torsie.

Elke niet-singuliere kromme op een glad oppervlak zal zijn raakvector $\mathbf {T}$ in het raakvlak van het oppervlak orthogonaal hebben liggen op de normaalvector. De normale kromming $k_{\text{n}}$ is de kromming van de kromme geprojecteerd op het vlak, dat de raakvector $\mathbf {T}$ van de kromme in het raakvlak van het oppervlak bevat en de normale $u$, van het oppervlak. De geodetische kromming, $k_{\text{g}}$ is de kromming van de kromme geprojecteerd op het raakvlak van het oppervlak en de geodetische torsie of relatieve torsie, $\tau _{\text{r}}$, meet de mate van verandering van de normaalvector van het oppervlak rond het raakvlak van de kromme.

Laat de kromme een eenheidssnelheidskromme zijn en $t=u\times \mathbf {T}$, zodat $\mathbf {T} ,u$ en $t$ een orthonormale basis vormen: het Darboux-frame. De bovenstaande grootheden zijn verbonden door:

${\begin{pmatrix}\mathbf {T'} \\\mathbf {t'} \\\mathbf {u'} \end{pmatrix}}={\begin{pmatrix}0&\kappa _{g}&\kappa _{n}\\-\kappa _{g}&0&\tau _{r}\\-\kappa _{n}&-\tau _{r}&0\end{pmatrix}}{\begin{pmatrix}\mathbf {T} \\\mathbf {t} \\\mathbf {u} \end{pmatrix}}$

Hoofdkromming

Zie Hoofdkromming voor het hoofdartikel over dit onderwerp.

Alle krommen met dezelfde raakvector zullen dezelfde normale kromming hebben, die dezelfde is als de kromming van de krommen die wordt verkregen door het oppervlak te doorsnijden met het vlak dat $\mathbf {T}$ en $u$ bevat. Rekening houdend met alle mogelijke raakvectoren worden de maximale en minimale waarden van de normale kromming op een punt de zogenaamde hoofdkrommingen, $k_{1}$ en $k_{2}$ genoemd, en worden de richtingen van de corresponderende raakvectoren hoofdrichtingen genoemd.

Twee dimensies: kromming van oppervlakken

Zie Differentiaalmeetkunde van oppervlakken voor het hoofdartikel over dit onderwerp.

Gaussiaanse kromming

Zie Gaussiaanse kromming voor het hoofdartikel over dit onderwerp.

In tegenstelling tot krommen, die geen intrinsieke, maar wel een extrinsieke kromming hebben (zij hebben alleen een kromming gegeven een inbedding), kunnen oppervlakken een intrinsieke kromming hebben, die onafhankelijk is van een inbedding. De Gaussiaanse kromming, vernoemd naar Carl Friedrich Gauss, is gelijk aan het product $k_{1}k_{2}$ van de hoofdkrommingen. Het heeft een dimensie van 1/lengte² en is positief voor boloppervlakken, negatief voor eenbladige hyperboloïden en nul voor vlakken. Het bepaalt of een oppervlak lokaal convex is (als de kromming positief is) of een lokaal zadelpunt is (als de kromming negatief is).

Deze definitie van Gaussiaanse kromming is extrinsiek in de zin dat het gebruikmaakt van de inbedding van het oppervlak in $\mathbb {R} ^{3}$ normaalvectoren, externe vlakken etc. Gaussiaanse kromming is echter in feite een intrinsieke eigenschap van het oppervlak, wat betekent dat het niet afhankelijk is van de bijzondere inbedding van het oppervlak; intuïtief betekent dit dat mieren die op het oppervlak leven de Gaussiaanse kromming kunnen bepalen. Een mier die op een boloppervlak leeft zou bijvoorbeeld de som van de inwendige hoeken van een driehoek kunnen meten en constateren dat deze groter is dan 180 graden, wat betekent dat de ruimte die die bewoont een positieve kromming heeft. Aan de andere kant zou een mier die op een cilinder leeft een dergelijke afwijking van de Euclidische meetkunde niet kunnen detecteren. Met name zou de mier niet kunnen detecteren dat dit oppervlak een andere gemiddelde kromming (zie hieronder) heeft dan een plat vlak, aangezien normale kromming een zuiver extrinsieke vorm van kromming is.

Formeel hangt de Gaussiaanse kromming alleen af van de Riemann-metriek van het oppervlak. Dit is Gauss zijn gevierde Theorema egregium, die hij vond in de periode dat hij actief was in geodetisch onderzoek en als kaartenmaker.

Een intrinsieke definitie van de Gaussiaanse kromming in een punt $P$ is de volgende: men stelt zich een mier voor die is vastgebonden aan punt $P$ met een korte draad van lengte $r.$ De mier loopt rond $P,$ terwijl de draad volledig is gespannen en meet de lengte $C(r)$ van een compleet rondje rondom $P.$ Als het oppervlak vlak zou zijn, zou de mier vinden dat $C(r)=2\pi r.$ Op gekromde oppervlakken, zal de formule voor $C(r)$ anders zijn, en kan de Gaussiaanse kromming $K$ op het punt $P$ worden berekend door gebruik te maken van de stelling van Bertrand-Diquet-Puiseux als

$K=\lim _{r\to 0}(2\pi r-C(r))\cdot {\frac {3}{\pi r^{3}}}$

De integraal van de Gaussiaanse kromming over het gehele oppervlak is nauw verwant aan het oppervlak van de Euler-karakteristiek, zie de stelling van Gauss-Bonnet.

Het discrete analogon van kromming, wat overeenkomt met kromming die wordt geconcentreerd op een punt en die in het bijzonder nuttig is voor veelvlakken, is het (angulaire) defect. Het analogon voor de stelling van Gauss-Bonnet is Descartes' stelling over het totale angulaire defect.

Omdat kromming kan worden gedefinieerd zonder verwijzing naar een inbeddende ruimte, is het om gekromd te zijn niet noodzakelijk dat een oppervlak in een hoger dimensionale ruimte is ingebed. Zulk een intrinsiek gekromd tweedimensionale oppervlak is een relatief eenvoudig voorbeeld van een Riemann-variëteit.

Gemiddelde kromming

De gemiddelde kromming is gelijk aan de helft van de som van de hoofdkrommingen, $(k_{1}+k_{2})/2.$ Het heeft de dimensie van 1/lengte. De gemiddelde kromming is nauw verwant aan de eerste variatie van oppervlakte. In het bijzonder heeft een minimaaloppervlak, zoals een zeepfilm een gemiddelde kromming van nul en heeft een zeepbel een constante gemiddelde kromming. In tegenstelling tot de Gaussiaanse kromming, is de gemiddelde kromming extrinsiek en hangt zij af van de inbedding in een hoger dimensionale ruimte. Een cilinder en een vlak zijn lokaal isometrisch, maar de gemiddelde kromming van een vlak is nul terwijl de gemiddelde kromming van een cilinder ongelijk aan nul is.

Tweede fundamentele vorm

De intrinsieke en extrinsieke kromming van een oppervlak kunnen in de tweede fundamentele vorm worden gecombineerd. Dit is een kwadratische vorm in het raakvlak aan het oppervlak op een punt waarvan de waarde op een bepaald raakvector $X$ aan het oppervlak de normale component van de versnelling van een kromme langs het raakvlak van het oppervlak dat raakt aan $X$ is; dat wil zeggen het is de normale kromming van een kromme rakend aan $X$ (zie hierboven). Symbolisch,

$I\!I(X,X)=N\cdot (\nabla _{X}X)$

waarin $n$ de eenheidnormaal op het oppervlak is. Voor eenheidsraakvectoren $X$ neemt de tweede fundamentele vorm de maximale waarde $k_{1}$ en minimale waarde $k_{2}$ aan, die zich respectievelijk voordoen in de hoofdrichtingen $u_{1}$ en $u_{2}.$ Dus door de hoofdasstelling is de tweede fundamentele vorm gelijk aan

$I\!I(X,X)=k_{1}(X\cdot u_{1})^{2}+k_{2}(X\cdot u_{2})^{2}$

De tweede fundamentele vorm codeert dus voor zowel de intrinsieke en extrinsieke kromming.

Een verwante notie van kromming is de vormoperator, een lineaire operator van het raakvlak op zichzelf. Wanneer de vormoperator wordt toegepast op een raakvector $X$ op het oppervlak, is de vormoperator de tangentiële component van de mate van verandering van de normaalvector, wanneer deze langs een kromme op het oppervlak dat raakt aan $X$ wordt bewogen. De hoofdkrommingen zijn de eigenwaarden van de vormoperator, en in feite hebben de vormoperator en de tweede fundamentele vorm dezelfde matrixweergave met betrekking tot een paar van orthonormale vectoren van het raakvlak. De Gaussiaanse kromming is dus de determinant van de vormtensor en de gemiddelde kromming is de helft van haar spoor.

Hogere dimensies: kromming van de ruimte

Door uitbreiding van het eerste argument kan een ruimte van drie of meer dimensies intrinsiek worden gebogen, de volledige wiskundige beschrijving wordt beschreven in kromming van Riemann-variëteiten. Ook hier kan de gekromde ruimte al of niet worden opgevat als zijnde ingebed in een hoger-dimensionale ruimte.

Na de ontdekking van de intrinsieke definitie van de kromming, die nauw verbonden is met de opgang van de niet-Euclidische meetkunde, hebben vele wis- en natuurkundigen zich afgevraagd of de gewone natuurkundige ruimte misschien gekromd kan zijn, dit hoewel het succes van de Euclidische meetkunde tot dat moment betekende dat de kromtestraal astronomisch groot moest zijn. In de theorie van de algemene relativiteitstheorie, die de zwaartekracht en kosmologie beschrijft, heeft het idee algemene vorm gekregen in de kromming van ruimte-tijd. In de relativiteitstheorie is de ruimtetijd een pseudo-Riemann-variëteit. Wanneer een tijdscoördinaat is gedefinieerd, is de drie-dimensionale ruimte die overeenkomt met een bepaalde tijdsmoment over het algemeen een gekromde Riemann-variëteit, maar aangezien de keuze van de tijdscoördinaten grotendeels willekeurig is, is het de onderliggende kromming van de ruimtetijd kromming die natuurkundige significant is.

Hoewel een willekeurig-gekromde ruimte zeer complex is om te beschrijven, wordt de kromming van een ruimte, die lokaal isotroop en homogeen is, beschreven door een enkele Gaussiaanse kromming. Wat betreft een oppervlak zijn er wiskundige strikte voorwaarden, maar deze corresponderen met redelijke natuurkundige aannames (alle punten en alle richtingen zijn niet van elkaar te onderscheiden). Een positieve kromming komt overeen met het omgekeerde kwadraat van de kromtestraal, een voorbeeld hiervan is een boloppervlak of hypersfeer. Een voorbeeld van een negatief gekromde ruimte is een hyperbolische meetkunde. Een ruimte of ruimtetijd met nulkromming noemt men plat. De euclidische ruimte is bijvoorbeeld een voorbeeld van een vlakke ruimte en de Minkowski-ruimte is een voorbeeld van een vlakke ruimtetijd. Er bestaan overigens ook andere voorbeelden van platte meetkunden. Aan een torus of een cilinder kan men beide vlakke metrieken toekennen, maar zij verschillen in hun topologie. Andere topologieën zijn ook mogelijk voor de gekromde ruimte. Zie ook vorm van het heelal.

Algemene beschrijving

Paralleltransport van een vector van $A\to N\to B$ geeft door de holonomie een andere vector.

Het wiskundige begrip kromming wordt ook in meer algemene context gedefinieerd. Veel van de beschrijvingen gaan over verschillende aspecten van de kromming, zoals deze in lagere dimensies worden begrepen.

Een van deze beschrijvingen is kinematisch. De kromming van een kromme kan worden beschouwd als een kinematische eenheid, die de kracht weergeeft, die door een bepaalde waarnemer, die zich langs de kromme verplaatst, wordt gevoeld. De kromming kan op dezelfde manier in hogere dimensies als een soort van getijdewerking worden beschouwd, dit is een manier om over sectiekromming na te denken. Deze beschrijving van de kromming hangt ervan af hoe dicht bij elkaar bevindende deeltjes divergeren of convergeren, wanneer zij zich vrij in de ruimte kunnen bewegen.

Een ander beschrijving van de kromming komt voort uit de studie van paralleltransport op een oppervlak. Als een vector bijvoorbeeld over een lus op een boloppervlak wordt verplaatst, waarbij het paralleltransport tijdens deze beweging behouden blijft, dan is de eindpositie van de vector niet hetzelfde als de beginpositie. Dit verschijnsel staat bekend als holonomie. Dit uit zich op verschillende manieren om de kromming als een maat voor de holonomie te beschrijven. Een nauw hieraan verwant begrip van kromming komt uit de ijktheorie in de natuurkunde, waar de kromming een veld bepaalt en een vectorpotentiaal voor het veld een grootheid is, die in het algemeen pad-afhankelijk is: de vectorpotentiaal kan veranderen als een waarnemer zich langs een lus beweegt.

Twee andere beschrijvingen van kromming zijn de scalaire kromming en de riccikromming. In een gekromd oppervlak, zoals op een boloppervlak, verschilt de oppervlakte van een schijf op dat oppervlak van de oppervlakte van een schijf met dezelfde straal in de vlakke ruimte. Dit verschil wordt, in een passende limiet, gemeten door de scalaire kromming. Het verschil in oppervlakte van een sector van de schijf wordt gemeten door de riccikromming. Zowel de scalaire- als de riccikromming worden op dezelfde manier in drie en hogere dimensies gedefinieerd. Ze zijn vooral belangrijk in de relativiteitstheorie, waar zij beide voorkomen aan de kant van einsteinvergelijkingen, die de meetkunde van de ruimtetijd weergeven. De andere kant van deze vergelijking geeft de aanwezigheid van materie en energie weer. Deze beschrijvingen van kromming liggen bijvoorbeeld ten grondslag aan het idee dat kromming een eigenschap van een maat kan zijn.

Een andere algemene vorm van kromming berust op het vermogen om een gekromde ruimte met een andere ruimte die een constante kromming heeft te vergelijken. Dit wordt vaak gedaan met driehoeken in de ruimten.