Besselfunctie
Besselfuncties zijn oplossingen van de besselse differentiaalvergelijking. Ze worden zo genoemd naar de wiskundige en astronoom Friedrich Wilhelm Bessel, die de vergelijking uitwerkte. Hij deed dit met het doel de verstoring te berekenen die drie hemellichamen op elkaars baan uitoefenen; voorbereidend werk was door anderen gedaan, maar Bessels vergelijking was meer algemeen geldig. Besselfuncties worden onderscheiden naar besselfuncties van de eerste soort en van de tweede soort. De besselfunctie van de eerste soort van de orde wordt genoteerd als , en die van de tweede soort van de orde als .
De besselvergelijking kan echter ook worden gebruikt om oplossingen te vinden voor de vergelijkingen van Laplace en van Helmholtz, wanneer daarbij cilindercoördinaten worden gebruikt. Daardoor zijn besselfuncties vooral van belang bij veel vraagstukken uit de wiskundige natuurkunde, zoals vragen omtrent golfvoortplanting, statische spanning enzovoort. Enkele voorbeelden zijn:
- elektromagnetische golven in een cilindrische golfgeleider
- warmtegeleiding in een cilindervormig voorwerp
- trillingswijzen van een dun cirkel- of ringvormig membraan
- verstrooiingsproblemen in een tralie.
- componentamplitudes bij frequentiemodulatie (FM): zie de grafiek Media:Bessels.png
- bepaling van grondwaterstanden bij onttrekkingen.
Definitie[bewerken | brontekst bewerken]
Besselfuncties zijn oplossingen van de besselse differentiaalvergelijking:
Oplossingen zijn en .
Voor zijn en lineair onafhankelijk, zodat voor de algemene oplossing geldt:
in het bijzonder is
Voor is
- ,
dus zijn en lineair afhankelijk.
Ook is
waarin
dus zijn ook en lineair afhankelijk. Wel zijn en lineair onafhankelijk, zodat in dit geval de algemene oplossing geschreven kan worden als
De besselfuncties van de eerste soort worden gegeven door de complexe integraal:
met een geschikte contour en de voortbrengende functie gegeven door:
Eigenschappen van de besselfunctie[bewerken | brontekst bewerken]
De besselfuncties van de eerste soort hebben de machtreeksontwikkeling
- ,
die met de methode van Frobenius afgeleid kan worden[1]
De besselfuncties voldoen aan de recursieve betrekkingen:
Een berekening leert dat de besselfunctie van de eerste soort en van de nulde orde gegeven wordt door:
Als we plotten dan verkrijgen we het volgende resultaat:
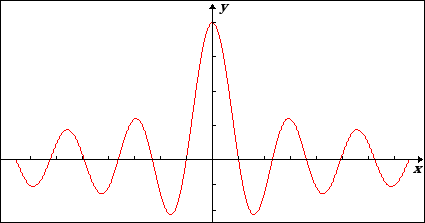
bereikt haar maximale amplitude in de oorsprong. Naarmate zich verwijdert van de oorsprong neemt de amplitude geleidelijk af om dan uiteindelijk te verdwijnen in het oneindige (, ).
Bronnen, noten en/of referenties
|
































