Continue functie (topologie)

In de topologie en aanverwante gebieden binnen de wiskunde is een continue functie een morfisme tussen topologische ruimten. Intuïtief is het een functie $f$ waar een verzameling van punten dicht bij $f(x)$ altijd het beeld van een verzameling van punten dicht bij $x$ bevat. Voor een algemene topologische ruimte betekent dit dat een omgeving van $f(x)$ altijd het beeld van een omgeving van $x$ bevat.

Dat houdt in dat in een metrische ruimte, zoals de reële getallen, de punten binnen een gegeven afstand van $f(x)$ altijd de beelden van alle punten binnen een zekere afstand van $x$ bevatten; dit wordt geformuleerd in de ε-δ definitie.

Definities

Er bestaan verschillende equivalente definities van een topologische ruimte, en dus zijn er ook verschillende equivalente manieren om een continue functie te definiëren.

Definities met open en gesloten verzamelingen

De meest gangbare definitie in de topologie van continue functie is als functie waarvan de originelen van open verzamelingen ook open zijn. Vergelijkbaar met de formulering in termen van open verzamelingen is die voor met gesloten verzamelingen, die stelt dat de originelen van gesloten verzamelingen ook gesloten zijn.

Definitie met omgevingen

Een functie $f$ van de topologische ruimte $X$ naar de topologische ruimte $Y$ heet continu in $x$, voor enige $x\in X$, als voor elke omgeving $V$ van $f(x)$ er een omgeving $U$ van $x$ bestaat zodanig dat $f(U)\subseteq V$. Als $f$ continu is op elke $x\in X$, dan zeggen we simpelweg dat $f$ continu is.

Hoewel deze definitie ingewikkeld lijkt, wordt hier intuïtief beweerd dat hoe "klein" $V$ ook mag worden, wij altijd een $U$, met daarin $x$, kunnen vinden die daarbinnen wordt afgebeeld.

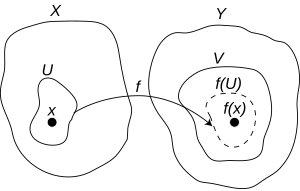
In een metrische ruimte zijn de open ballen, rond $x$ en $f(x)$ de omgevingen. Dit leidt tot de standaard ε-δ-definitie van een continue functie uit de reële analyse, die ruwweg zegt dat een functie continu is, indien alle punten dicht bij $x$ op punten dicht bij $f(x)$ afgebeeld worden. Deze omschrijving heeft alleen betekenis in een metrische ruimte, waar een begrip afstand is gedefinieerd.

Is de beeldruimte een Hausdorff-ruimte, dan is $f$ dan en slechts dan continu in $a$ als de limiet van $f(x)$, als $x$ tot $a$ nadert, gelijk is $f(a)$. Op een geïsoleerd punt is iedere functie continu.