Gebruiker:KoenB/Kladblok

Tabel op en:

Tabel met projecties

Projectie	Afbeeldingen	Type	Eigenschappen	Bedenker	Jaartal	Notities
Kadratische platkaart = equidistante cilinderprojectie		Cylindrisch	Afstandsgetrouw	Marinus van Tyrus	120	Eenvoudige afbeelding van geografische lengte en breedte; afstandsgetrouw langs de meridianen.
Mercator = Wright		Cylindrisch	Hoekgetrouw	Gerardus Mercator	1569	Lijnen van constante kompaskoers zijn rechten, wat van nut is voor navigatie. De schaal neemt af met de afstand tot de evenaar, zodanig dat de polen niet in beeld kunnen komen.
Braun vergelijkbaar met James Gall		Cylindrisch	Compromis	Carl Braun	1867	Geïnspireerd op de Mercatorprojectie, maar dan met de polen in beeld. De standaardparallel is hier de evenaar; James Gall heeft deze op 45° N/Z.
Orthografische cilinderprojectie van Lambert		Cylindrisch	Oppervlaktegetrouw	Johann Heinrich Lambert	1772	Rakend aan de evenaar. Kaartverhouding 1 : 3.14 (pi).
Gall–Peters		Cylindrisch	Oppervlaktegetrouw	James Gall (Arno Peters)	1855	Verticaal uitgerekte versie van de orthografische cilinderprojectie van Lambert. Snijdend door de parallellen 45° N/Z. De Balthasartprojectie is een variant hierop, snijdend door de 50°-parallellen.
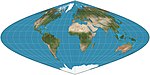
Sinusoidal = Sanson-Flamsteed = Mercator equal-area		Pseudocylindrical	Equal-area	(Several; first is unknown)	1600 (c.)	Meridians are sinusoids; parallels are equally spaced. Aspect ratio of 2:1. Distances along parallels are conserved.
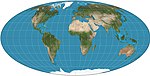
Mollweide = elliptical = Babinet = homolographic		Pseudocylindrical	Equal-area	Karl Brandan Mollweide	1805	Meridians are ellipses.
Eckert II		Pseudocylindrical	Equal-area	Max Eckert-Greifendorff	1906
Eckert IV		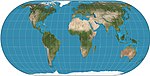Pseudocylindrical	Equal-area	Max Eckert-Greifendorff	1906	Parallels are unequal in spacing and scale; outer meridians are semicircles; other meridians are semiellipses.
Eckert VI		Pseudocylindrical	Equal-area	Max Eckert-Greifendorff	1906	Parallels are unequal in spacing and scale; meridians are half-period sinusoids.
Ortelius oval		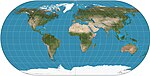Pseudocylindrical		Battista Agnese	1540	Meridians are circular.
Goode homolosine		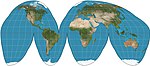Pseudocylindrical	Equal-area	John Paul Goode	1923	Hybrid of Sinusoidal and Mollweide projections. Usually used in interrupted form.
Kavrayskiy VII		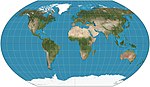Pseudocylindrical	Compromise	Vladimir V. Kavrayskiy	1939	Evenly spaced parallels. Equivalent to Wagner VI horizontally compressed by a factor of ${\sqrt {3}}/{2}$.
Robinson		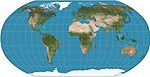Pseudocylindrical	Compromise	Arthur H. Robinson	1963	Computed by interpolation of tabulated values. Used by Rand McNally since inception and used by NGS 1988–98.
Natural Earth		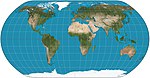Pseudocylindrical	Compromise	Tom Patterson	2011	Computed by interpolation of tabulated values.
Tobler hyperelliptical		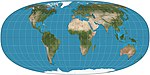Pseudocylindrical	Equal-area	Waldo R. Tobler	1973	A family of map projections that includes as special cases Mollweide projection, Collignon projection, and the various cylindrical equal-area projections.
Wagner VI		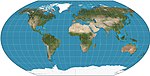Pseudocylindrical	Compromise	K.H. Wagner	1932	Equivalent to Kavrayskiy VII vertically compressed by a factor of ${\sqrt {3}}/{2}$.
Collignon		Pseudocylindrical	Equal-area	Édouard Collignon	1865 (c.)	Depending on configuration, the projection also may map the sphere to a single diamond or a pair of squares.
HEALPix		Pseudocylindrical	Equal-area	Krzysztof M. Górski	1997	Hybrid of Collignon + Lambert cylindrical equal-area
Boggs eumorphic		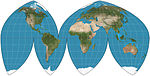Pseudocylindrical	Equal-area	Samuel Whittemore Boggs	1929	The equal-area projection that results from average of sinusoidal and Mollweide y-coordinates and thereby constraining the x coordinate.
Craster parabolic =Putniņš P4		Pseudocylindrical	Equal-area	John Craster	1929	Meridians are parabolas. Standard parallels at 36°46′N/S; parallels are unequal in spacing and scale; 2:1 Aspect.
Flat-polar quartic = McBryde-Thomas #4		Pseudocylindrical	Equal-area	Felix W. McBryde, Paul Thomas	1949	Standard parallels at 33°45′N/S; parallels are unequal in spacing and scale; meridians are fourth-order curves. Distortion-free only where the standard parallels intersect the central meridian.
Quartic authalic		Pseudocylindrical	Equal-area	Karl Siemon Oscar Adams	1937 1944	Parallels are unequal in spacing and scale. No distortion along the equator. Meridians are fourth-order curves.
The Times		Pseudocylindrical	Compromise	John Muir	1965	Standard parallels 45°N/S. Parallels based on Gall orthographic, but with curved meridians. Developed for Bartholomew Ltd., The Times Atlas.
Loximuthal		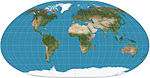Pseudocylindrical		Karl Siemon, Waldo Tobler	1935, 1966	From the designated centre, lines of constant bearing (rhumb lines/loxodromes) are straight and have the correct length. Generally asymmetric about the equator.
Aitoff		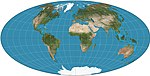Pseudoazimuthal	Compromise	David A. Aitoff	1889	Stretching of modified equatorial azimuthal equidistant map. Boundary is 2:1 ellipse. Largely superseded by Hammer.
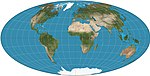
Hammer = Hammer-Aitoff variations: Briesemeister; Nordic		Pseudoazimuthal	Equal-area	Ernst Hammer	1892	Modified from azimuthal equal-area equatorial map. Boundary is 2:1 ellipse. Variants are oblique versions, centred on 45°N.
Winkel tripel		Pseudoazimuthal	Compromise	Oswald Winkel	1921	Arithmetic mean of the equirectangular projection and the Aitoff projection. Standard world projection for the NGS 1998–present.
Van der Grinten		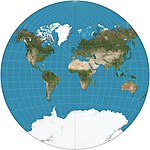Other	Compromise	Alphons J. van der Grinten	1904	Boundary is a circle. All parallels and meridians are circular arcs. Usually clipped near 80°N/S. Standard world projection of the NGS 1922–88.
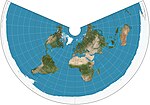
Equidistant conic projection = simple conic		Conic	Equidistant	Based on Ptolemy’s 1st Projection	100 (c.)	Distances along meridians are conserved, as is distance along one or two standard parallels
Lambert conformal conic		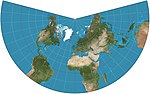Conic	Conformal	Johann Heinrich Lambert	1772
Albers conic		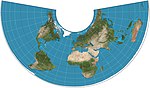Conic	Equal-area	Heinrich C. Albers	1805	Two standard parallels with low distortion between them.
Werner		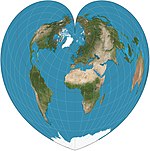Pseudoconical	Equal-area	Johannes Stabius	1500 (c.)	Distances from the North Pole are correct as are the curved distances along parallels.
Bonne		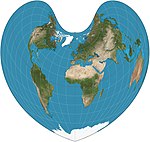Pseudoconical, cordiform	Equal-area	Bernardus Sylvanus	1511	Parallels are equally spaced circular arcs and standard lines. Appearance depends on reference parallel. General case of both Werner and sinusoidal
Bottomley		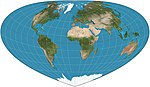Pseudoconical	Equal-area	Henry Bottomley	2003	Alternative to the Bonne projection with simpler overall shape Parallels are elliptical arcs Appearance depends on reference parallel.
American polyconic		Pseudoconical		Ferdinand Rudolph Hassler	1820 (c.)	Distances along the parallels are preserved as are distances along the central meridian.
Azimuthal equidistant =Postel zenithal equidistant		Azimuthal	Equidistant	Abū Rayḥān al-Bīrūnī	1000 (c.)	Used by the USGS in the National Atlas of the United States of America. Distances from centre are conserved. Used as the emblem of the United Nations, extending to 60° S.
Gnomonic		Azimuthal	Gnomonic	Thales (possibly)	580 BC (c.)	All great circles map to straight lines. Extreme distortion far from the center. Shows less than one hemisphere.
Lambert azimuthal equal-area		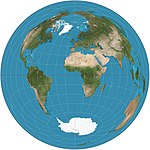Azimuthal	Equal-area	Johann Heinrich Lambert	1772	The straight-line distance between the central point on the map to any other point is the same as the straight-line 3D distance through the globe between the two points.
Stereographic		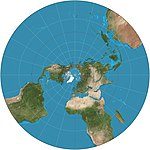Azimuthal	Conformal	Hipparchos (deployed)	200 BC (c.)	Map is infinite in extent with outer hemisphere inflating severely, so it is often used as two hemispheres. Maps all small circles to circles, which is useful for planetary mapping to preserve the shapes of craters.
Orthographic		Azimuthal		Hipparchos (deployed)	200 BC (c.)	View from an infinite distance.
Vertical perspective		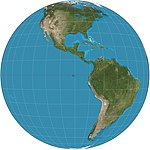Azimuthal		Matthias Seutter (deployed)	1740	View from a finite distance. Can only display less than a hemisphere.
Two-point equidistant		Azimuthal	Equidistant	Hans Maurer	1919	Two "control points" can almost be arbitrarily chosen. The two straight-line distances from any point on the map to the two control points are correct.
Peirce quincuncial		Other	Conformal	Charles Sanders Peirce	1879
Guyou hemisphere-in-a-square projection		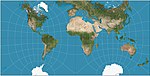Other	Conformal	Émile Guyou	1887
Adams hemisphere-in-a-square projection		Other	Conformal	Oscar Sherman Adams	1925
B.J.S. Cahill's Butterfly Map		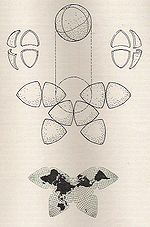Polyhedral	Compromise	Bernard Joseph Stanislaus Cahill	1909	Projects the globe onto an octahedron with symmetrical components and contiguous landmasses that may be displayed in various arrangements
Cahill-Keyes projection		Polyhedral	Compromise	Gene Keyes	1975	Projects the globe onto a truncated octahedron with symmetrical components and contiguous land masses
Waterman butterfly projection		Polyhedral	Compromise	Steve Waterman	1996	Projects the globe onto a truncated octahedron with symmetrical components and contiguous land masses that may be displayed in various arrangements
Quadrilateralized spherical cube		Polyhedral	Equal-area	F. Kenneth Chan, E. M. O’Neill	1973
Dymaxion map		Polyhedral	Compromise	Buckminster Fuller	1943	Also known as a Fuller Projection.
Myriahedral projections		Polyhedral	Compromise	Jarke J. van Wijk	2008	Projects the globe onto a myriahedron: a polyhedron with a very large number of faces.
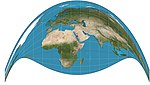
Craig retroazimuthal = Mecca			Retroazimuthal	James Ireland Craig	1909
Hammer retroazimuthal, front hemisphere			Retroazimuthal	Ernst Hammer	1910
Hammer retroazimuthal, back hemisphere			Retroazimuthal	Ernst Hammer	1910
Littrow		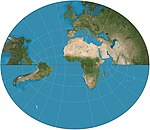	Retroazimuthal	Joseph Johann Littrow	1833	Also conformal
Armadillo		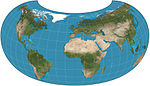Other	Compromise	Erwin Raisz	1943