Stelling van Thales (rechten)
De stelling van Thales voor rechten is een meetkundige stelling, geformuleerd door de wiskundige en filosoof Thales van Milete, omstreeks 624 v.Chr. - 545 v.Chr. Thales gebruikte volgens de legende deze stelling om de hoogte van de piramiden in het oude Egypte te berekenen. Hij maakte daarbij gebruik van de lengte van de schaduw van iedere piramide en de lengte van de schaduw van een stok met een bekende lengte.
Verschillende stellingen van Thales[bewerken | brontekst bewerken]
De stelling van Thales voor rechten gaat over de verhouding tussen de lengte van lijnstukken op twee willekeurige rechten die door drie andere evenwijdige rechten worden gesneden. Er is een andere stelling van Thales, voor cirkels, die zegt dat een driehoek ingeschreven in een cirkel, waarvan één zijde een middellijn van de cirkel vormt, een rechthoekige driehoek is.
Stelling van Thales voor rechten[bewerken | brontekst bewerken]

De stelling van Thales voor rechten zegt:
Als drie evenwijdige lijnen twee andere lijnen en snijden, lijn in de punten A, B en C, en lijn in A', B' en C', waarbij A en A' op de ene, B en B' op de tweede en C en C' op de derde van de evenwijdige lijnen liggen, dan is:
De vergelijkingen kunnen ook worden geschreven als:
Dit betekent dat de verhouding tussen de lengte van twee lijnstukken op een lijn die de projecties zijn van twee lijnstukken op een andere lijn , hetzelfde is als de verhouding van de twee lijnstukken op .
Bepaling van de hoogte van piramiden[bewerken | brontekst bewerken]
De legende wil dat Thales, tijdens een reis naar Egypte, de piramiden bezocht die enkele eeuwen voorheen waren gebouwd. Hij vond het prachtige bouwwerken en wilde de hoogte van de Piramide van Cheops berekenen.
Hij probeerde dit met behulp van gelijkvormige driehoeken en zijn stelling. Hij bepaalde de verhouding tussen de hoogte van de piramide en de lengte van de schaduw van de piramide aan de hand van een paal die naast de piramide stond.
De lengte van de schaduw van de piramide kon hij berekenen. Hij merkte op dat de zonnestralen twee keer op een dag loodrecht op een zijde van de piramide stonden. Het volstond dus de lengte van de schaduw tot de voet van de piramide te meten en daar de helft van de lengte van een zijde bij te tellen.

Thales mat de piramide en de hoogte van de paal op.
- hoogte van de paal: 1,63 m
- schaduw van de paal: 2 m
- basislengte aan de voet van de piramide: 230 m
- schaduw van de piramide: 65 m
Dus:
en:
Andere vormen[bewerken | brontekst bewerken]
 |
 |
De stelling van Thales blijft geldig als een puntenpaar samenvalt met het snijpunt van de twee lijnstukken. De stelling van Thales geldt in de snavelfiguur en de zandloperfiguur nog steeds:
Omgekeerde[bewerken | brontekst bewerken]
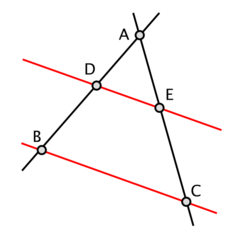
Als in de driehoek ABC de punten D op AB en E op AC zo liggen dat
- ,
dan is DE evenwijdig aan BC.













