Markovketen
Een markovketen, genoemd naar de Russische wiskundige Andrej Markov, beschrijft een systeem dat zich door een aantal toestanden beweegt en stapsgewijs overgangen vertoont van de ene naar een andere (of dezelfde) toestand. De specifieke markov-eigenschap houdt daarbij in dat populair uitgedrukt: "de toekomst gegeven het heden niet afhangt van het verleden". Dat betekent dat als het systeem zich in een bepaalde toestand bevindt, het toekomstige gedrag van het systeem, dus de komende overgangen, slechts afhangen van de huidige toestand en niet van de weg waarlangs deze toestand tot stand is gekomen. De toestanden van het systeem worden beschreven door een rij stochastische variabelen met kansverdelingen , waarin de toestand van het systeem is na stappen. De markov-eigenschap wordt uitgedrukt in een eigenschap van de overgangskansen.
Een markovketen kan met een stochastische matrix worden weergegeven.
Definitie
[bewerken | brontekst bewerken]Een markovketen van een systeem met mogelijke toestanden is een discreet stochastisch proces met waarden in dat voldoet aan de markov-eigenschap.
De kansverdeling van wordt gegeven door de kansfunctie over waarvoor geldt:
De begintoestand van het systeem wordt gegeven door de beginverdeling . Tussen de kansverdelingen bestaat de relatie
waarin de kansverdelingen beschouwd worden als rijvector en de matrix van overgangskansen op is met elementen
Het getal is de kans dat het systeem op overgaat van toestand naar toestand . Anders gezegd: dit is de voorwaardelijke kans dat het systeem op zeker tijdstip zich bevindt in toestand , gegeven dat het systeem zich op tijdstip in toestand bevond. Hiervoor geldt de markov-eigenschap, die zegt dat deze kans alleen afhangt van de toestand op tijdstip en niet van de daaraan voorafgaande toestanden:
Het systeem heeft met andere woorden geen 'geheugen'. Men noemt dit een markovketen van de eerste orde in discrete tijd: het systeem kan alleen van toestand veranderen op regelmatige tijdstippen.
Eigenschappen
[bewerken | brontekst bewerken]- Er geldt altijd dat , maar kan van 1 verschillen. De figuren illustreren dat.
Generalisaties
[bewerken | brontekst bewerken]De definitie van markovketen kan op verschillende manieren gegeneraliseerd worden:
- Het systeem kan een oneindig aantal discrete toestanden aannemen of een continue toestandsruimte bezitten, zoals bij de brownse beweging. Als de toestandsruimte continu is, spreekt men van een markovproces en niet van een markovketen; maar de termen worden vaak door elkaar gebruikt.
- De eenstapsovergangskansen kunnen afhankelijk zijn van het tijdstip . Als de overgangskansen niet variëren in de tijd noemt men de markovketen homogeen;
- Men kan een markovketen van orde beschouwen waarvan de eenstapsovergangskansen niet alleen afhangen van de vorige toestand, maar van vorige toestanden ():
- In plaats van een systeem dat alleen op regelmatige, discrete tijdstippen verandert, kan men ook een systeem beschouwen in continue tijd, dat op onregelmatige tijdstippen van toestand verandert.
Voorbeelden
[bewerken | brontekst bewerken]Voorbeeld 1
[bewerken | brontekst bewerken]Een muis beweegt zich door een huis met op de bovenverdieping de vertrekken 1, ..., 5 en op de benedenverdieping de vertrekken 6, 7 en 8. Hij kan zich vrij op de bovenverdieping door de vertrekken bewegen, maar mocht hij in de slaapkamer 5 door het gat in de vloer vallen, dan is er geen weg terug en is hij gedwongen beneden te blijven. In de keuken, kamer nummer 8, staat een val, waar de muis, mocht hij zich in de keuken wagen, beslist in terechtkomt. Op zoek naar eten loopt de muis rond en weet zich echt niet te herinneren of hij al in een vertrek is geweest. Hij kiest daarom steeds met gelijke kansen naar een van de aangrenzende vertrekken te gaan.
De weg die de muis aflegt laat zich met een gewogen, gerichte graaf beschrijven:
Een verloop kan zijn dat de muis zich aan het begin in kamer 5 bevindt en van daaruit naar een van de vertrekken 2, 3, 4 en 7 gaat, met voor alle vier een kans van 1/4. De weg van de muis kan er zo uitzien: 5 4 1 4 1 2 5 7 6 7 8 of met meer geluk: 5 4 1 2 5 4 1 2 3 2 1 4 1 4 1 4 1 4 1 2 3 5 7 6 7 6 7 6 7 8.
Voor de bovenstaande graaf is dit de overgangs- of transitiematrix:
Zoals hierboven gezegd is in het getal op rij en kolom de kans dat het systeem van toestand naar toestand overgaat, hier dus de kans dat de muis van kamer naar kamer gaat. Dit zijn de getallen bij de pijlen in de gegeven graaf. is een stochastische matrix: iedere rij van de matrix bestaat uit getallen tussen 0 en 1 en de som van elke rij is gelijk aan 1.
De kans dat de muis vanuit kamer 5 precies het pad 5 4 1 4 1 2 5 7 6 7 8 volgt kan aan de hand van deze matrix worden berekend, het is de combinatie van de overgangskansen 5→4, 4→1, 1→4, 4→1 enzovoort. Deze kans is het product van de overgangskansen:
De verwachte toestand van het systeem op tijdstip wordt beschreven door een rijvector . Het aantal elementen van deze vector is in dit geval gelijk aan het aantal kamers en het -de element in de vector is de kans dat de muis zich op tijdstip in kamer bevindt.
Stel dat de muis bij tijdstip 0 in kamer 5 verblijft, dan is de beginverdeling
Vanuit kamer 5 kan de muis gaan naar de kamers 2, 3, 4 of 7. De kans daar op is steeds gelijk aan 1/4. Dit betekent dat op tijdstip 1 de muis met een kans gelijk aan 1/4 in een van de kamers 2, 3, 4 en 7 zit en met kans 0 in de andere kamers. Dus
Deze verdeling ontstaat als het matrixproduct van de rijvector met de stochastische matrix .
De kansverdeling op tijdstip 2 ontstaat op dezelfde manier
In het algemeen geldt
Na honderd stappen is de toestandsvector geëvolueerd tot
- .
Hoe verder in de tijd, hoe waarschijnlijker het wordt dat de muis in kamer 8 terechtkomt, vanwaar er geen uitweg is. Dit volgt uit de 1 in de hoofddiagonaal van de stochastische matrix ). De toestandsvector is voor stijgende in de limiet invariant, dus geldt er
zodat
- .
Dat betekent dat de muis in de limiet altijd in kamer 8 eindigt. Deze asymptotische verdeling is onafhankelijk van de begintoestand : waar de muis zich ook bevond bij de aanvang, ooit komt hij in kamer 8 terecht en daar niet meer uit kunnen. Die limietkans is voor de andere kamers gelijk aan 0, wat betekent dat de muis daar na een voldoend lange tijd niet meer is. Dergelijke toestanden worden overgangstoestanden[1] genoemd en een toestand zoals dat de muis in kamer 8 zit een absorberende toestand.[2]
Een markovketen met de eigenschap, dat de kansverdeling in de limiet onafhankelijk is van de begintoestand, noemt men compleet ergodisch.
Stel nu dat er in een ander huis twee muizenvallen zijn, bijvoorbeeld in kamers 4 en 8. De transitiematrix zal er dan anders uitzien dan hierboven, en tweemaal een 1 hebben op de hoofddiagonaal, in rijen 4 en 8. In dat geval is de markovketen niet meer compleet ergodisch. In sommige gevallen zal de muis in de val lopen in kamer 4 en in sommige gevallen in kamer 8. De limietverdeling is hier dus niet meer onafhankelijk van de begintoestand.
De limietvector is een eigenvector van de overgangsmatrix, overeenkomend met de eigenwaarde 1. De stelling van Perron-Frobenius zegt dat iedere stochastische matrix minstens een zo'n vector heeft en dat 1 de grootste eigenwaarde is van de matrix. Een stochastische matrix kan meer limietvectoren hebben, zoals in het geval van een markovketen met verschillende absorberende toestanden. De voorwaarde is dat de matrix of de corresponderende markovketen irreducibel is. Daarvoor moet iedere toestand vanuit iedere andere toestand kunnen worden bereikt, er mogen geen delen van de graaf geïsoleerd zijn van andere delen.
Voorbeeld 2
[bewerken | brontekst bewerken]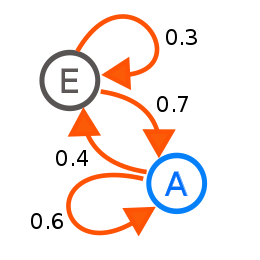
De hiernaast afgebeelde graaf stelt een markovketen voor met twee toestanden, A en E. Als het systeem zich op een bepaald tijdstip in toestand A bevindt, is de kans dat het zich op het volgende tijdstip nog steeds in toestand A bevindt, gelijk aan 0,6; de kans dat het overgaat naar toestand E is gelijk aan 0,4. Als het systeem zich in toestand E bevindt, is de kans dat het overgaat naar toestand A groter: 0,7. De stochastische matrix voor dit systeem met toestanden A en E is:
Stel dat het systeem vertrekt vanuit toestand A; dan is . In de volgende stappen vinden we voor de toestandsvector:
- , enz.
Als het systeem vertrekt vanuit toestand E, is . Nu vinden we in de volgende stappen:
- , enz.
Klaarblijkelijk evolueert , voor stijgende , hier ook naar een constante vector die onafhankelijk is van de begintoestand van het systeem. Wat is die vector ? Om die te vinden moeten we de vergelijking oplossen. Samen met de eis dat de som van de elementen van gelijk is aan 1, vormt dit een stelsel van lineaire vergelijkingen. Stel
- ,
dan is dat een stelsel van drie vergelijkingen in twee onbekenden:
(Een van de drie vergelijkingen is lineair afhankelijk van de andere twee). Door bijvoorbeeld te vervangen door in de eerste vergelijking, vinden we dat en dus is
- en
Op lange termijn is de kans het grootst (namelijk 7/11) dat we het systeem aantreffen in toestand A. We hebben hier dus ook te maken met een compleet ergodisch proces, maar dan een zonder overgangstoestanden. De toestanden A en E zijn recurrente toestanden, die met zekerheid een oneindig aantal malen zullen voorkomen als naar oneindig gaat. Een markovketen zoals deze, waarin elke toestand recurrent is, noemt men een recurrente keten.
We kunnen hier ook de kans berekenen dat het systeem zich in een toestand bevindt en exact tijdstippen in dezelfde toestand blijft; dus dat het de volgorde doorloopt waarin er maal een "overgang" van naar gebeurt gevolgd door een overgang van naar , waarin verschilt van . Die kans is:
De kans dat het systeem zich in toestand A bevindt en daar gedurende vijf opeenvolgende tijdstippen blijft en dan naar toestand E overgaat is dus gelijk aan 0,64.(1−0,6) = 0,05184.
Het verwachte aantal opeenvolgende gelijke toestanden, dus de verwachte duur dat het systeem in eenzelfde toestand blijft, is dan gelijk aan:
In dit geval is dit voor toestand A : 1/(1−0,6) = 2,5 en voor toestand E: 1/(1−0,3) = 1,4286. Over een (oneindig) lange periode verwachten we dat het systeem gemiddeld 2,5 tijdsperioden in toestand A blijft en 1,4286 tijdsperioden in toestand E.
Voorbeeld 3: toevalsbeweging
[bewerken | brontekst bewerken]
Een toevalsbeweging in een netwerk of een rooster is een typische markovketen. Stel dat het netwerk een binaire boom is zoals hiernaast afgebeeld, waarin een vlo voortdurend verspringt van een knooppunt naar een willekeurig aangrenzend knooppunt; zowel omhoog als omlaag (met de richting van de pijlen houden we geen rekening). De overgangsmatrix voor dit systeem met negen mogelijke toestanden, is:
De limietvector voor dit systeem laat zich eenvoudig berekenen; het is
Deze waarden zijn evenredig met het aantal verbindingen van en naar de knooppunten in de boom.
Maar als we de kansvector () berekenen voor het geval de vlo start vanuit knooppunt 1, vinden we dat die na verloop van tijd niet naar die waarde gaat maar blijft oscilleren tussen de twee waarden:
- in de even stappen, en
- in de oneven stappen.
Als de vlo vertrekt vanuit knooppunt 2 of 3 is de volgorde van deze twee vectoren omgekeerd. Dit is uiteraard het gevolg van het feit dat de vlo op elk tijdstip van niveau verandert in de boom. Als ze op tijdstip 0 op een "even" niveau begint zal ze op elk volgend even tijdstip ook op een even niveau zijn, en is de kans dat ze zich op een knooppunt van een oneven niveau bevindt noodzakelijkerwijs nul. De limietvector die hierboven berekend is, kunnen we beschouwen als de kans dat de vlo zich op een bepaald knooppunt bevindt op een willekeurig tijdstip in de toekomst.
Als we toelaten dat de vlo mag "rusten" op sommige punten, valt deze oscillatie weg en zal de toestandsvector evolueren naar een vaste limietwaarde. Na een groot aantal sprongen kan de vlo dan immers op elk knooppunt van de boom zitten. In dat geval zullen sommige waarden op de hoofddiagonaal van de overgangsmatrix verschillend van nul zijn.
Toepassingen
[bewerken | brontekst bewerken]Markovketens en markovprocessen worden in velerlei domeinen gebruikt voor het simuleren en analyseren van (computer)modellen van systemen waarvan de toestand geheel of gedeeltelijk van het toeval afhangt. Afhankelijk van de aard van het probleem wordt daarbij het transiënt gedrag van de keten dan wel de limiettoestand onderzocht.
- In de scheikunde kan het klassieke model van de kinetiek van enzym-gekatalyseerde reacties, beschreven door de Michaelis-Mentenvergelijking, voorgesteld worden als een markovketen. Ook de groei en samenstelling van copolymeerketens kan met markovketens geanalayseerd worden.
- In de wachtrijtheorie kan men markovketens inzetten voor het analyseren van wachtrijproblemen en het optimaliseren van telecommunicatienetwerken.
- In de economische en financiële wereld komen markovketens veelvuldig voor bij het modelleren van allerlei fenomenen, zoals bij Leontiefs input-outputanalyse. Het economische aspect komt bijvoorbeeld aan bod als aan een overgang van het systeem een bepaalde opbrengst (positief of negatief, winst of verlies) verbonden is. Men kan dan bepalen wat de verwachte opbrengst is in de volgende stappen, in functie van de huidige toestand van het systeem (transiënt gedrag), of wat de verwachte opbrengst per stap is op lange termijn.
- De statistiek combineert markovketens met Monte-Carlosimulaties in de zogenaamde MCMC-methode (Markov Chain Monte Carlo). Hierbij onderzoekt men steekproefsgewijs hoeveel stappen er nodig zijn om een vooraf bepaalde, stationaire verdeling van een markovketen te bereiken of te benaderen binnen een bepaalde foutenmarge. De methode wordt o.m. toegepast om meerdimensionale integralen numeriek te berekenen.
- In kwaliteitsmanagement voor het bepalen van de betrouwbaarheid en beschikbaarheid van systemen, bijvoorbeeld van procescontrole- of regelsystemen.
- Veel spellen waarin het toeval een rol speelt kunnen als een markovketen gemodelleerd worden.
- In de muziek kunnen markovketens dienen als basis voor stochastische muziek, zoals bij Iannis Xenakis.
- Bij het berekenen van kans op wolkenvorming worden markovketens toegepast.[3]
- In taalmodellen met kunstmatige intelligentie wordt gebruik gemaakt van de markov-eigenschap.
- Een hidden Markov model is een markovproces met onwaarneembare toestanden. De uitkomsten van het proces hangen op bekende wijze af van een waarneembaar proces en wel zo dat op een bepaald tijdstip de toestand van dit waarneembare proces alleen afhangt van de toestand van de onwaarneembare toestand van het verborgen markovproces. Het doel is kennis over het verborgen proces te verkrijgen op basis van het waarneembare proces.
- ↑ Engels: transient state
- ↑ Engels: absorbing state of trapping state
- ↑ promotie-onderzoek van Jesse Dorrestijn voor het Centrum Wiskunde & Informatica





































































