Negenpuntscirkel
Uiterlijk
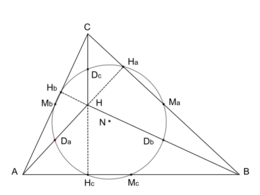


Van de driehoek ΔABC is de negenpuntscirkel de cirkel door de volgende negen punten:
- de middens van de zijden van de driehoek: Ma, Mb en Mc,
- de hoekpunten van de voetpuntsdriehoek van ΔABC: Ha, Hb en Hc en
- de middens van de lijnstukken die het hoogtepunt H verbinden met de hoekpunten: Da, Db en Dc.
De driehoek MaMbMc met zijden die de helft zijn van de zijden van ΔABC, is gelijkvormig met deze driehoek. De negenpuntscirkel is de omgeschreven cirkel van ΔMaMbMc, dus heeft als straal de helft van de straal van de omgeschreven cirkel van ΔABC.
De zijden van ΔDaDbDc zijn de helft van de zijden van ΔABC, dus is ΔDaDbDc ook gelijkvormig met ΔABC.
Stelling van Feuerbach[bewerken | brontekst bewerken]
De Duitse wiskundige Karl Feuerbach 1800-1834 bewees in 1822 dat de negenpuntscirkel aan de ingeschreven cirkel en de aangeschreven cirkels van een driehoek raakt. Het raakpunt met de ingeschreven cirkel heet punt van Feuerbach en de raakpunten met de aangeschreven cirkels vormen de driehoek van Feuerbach.
Overige[bewerken | brontekst bewerken]
- Het middelpunt van de negenpuntscirkel ligt op de rechte van Euler.
- De negenpuntscirkel is de omgeschreven cirkel van ΔDaDbDc en is het beeld van de omgeschreven cirkel van ΔABC bij vermenigvuldiging met de factor 1/2 en centrum H. De negenpuntscirkel gaat dus door het midden van elk lijnstuk HP, waarbij P op de omgeschreven cirkel van ΔABC ligt. Met andere woorden: de negenpuntscirkel is de meetkundige plaats van de middens G van de lijnstukken HP. De drie voetpunten van ieder punt P op de omschreven cirkel van ΔABC op de drie zijden van ΔABC en het midden G tussen H en P liggen op een lijn, op de rechte van Wallace.
- Het middelpunt N van de negenpuntscirkel ligt op de rechte van Euler en de cirkel van Lester. Het is het driehoekscentrum met kimberlingnummer X(5). De barycentrische coördinaten van N zijn
Websites[bewerken | brontekst bewerken]
- MJG Scheer. A simple vector proof of Feuerbach’s theorem, 2011. in Forum Geometricorum 11, blz 205-210.

