Wet van Planck

De wet van Planck, ook wel stralingswet van Planck genoemd, beschrijft de intensiteitsverdeling van de straling respectievelijk de dichtheidsverdeling van de fotonen, als functie van de golflengte respectievelijk van de frequentie, van de door een zwarte straler – een ideale stralingsbron – bij een bepaalde temperatuur uitgestraalde elektromagnetische golven.
Toen Max Planck in 1900 de stralingswet afleidde, bleek dat een beschrijving vanuit de klassieke natuurkunde niet mogelijk is.[1] Het bleek nodig een nieuw postulaat in te voeren, dat stelt dat energie-uitwisseling tussen oscillatoren en het elektromagnetische veld niet continu, maar in de vorm van kleine energiepakketjes (later kwanta of kwanten genoemd) plaatsvindt. Plancks afleiding van de stralingswet wordt wel gezien als de geboorte van de kwantummechanica en wordt gerekend tot de "oude" kwantumtheorie.
Achtergrond en betekenis[bewerken | brontekst bewerken]

Volgens de stralingswet van Kirchhoff zijn voor ieder lichaam en voor iedere golflengte het absorptievermogen en het emissievermogen voor warmtestraling onderling evenredig. Een zwart lichaam is een hypothetisch lichaam dat invallende straling bij elke golflengte en intensiteit volledig absorbeert. Daar zijn absorptievermogen voor iedere golflengte de maximale waarde heeft, zal ook zijn emissievermogen bij elke golflengte de maximale waarde hebben. Een reëel lichaam kan bij geen enkele golflengte meer straling uitzenden dan een zwart lichaam, zodat deze laatste als model voor een ideale stralingsbron geldt. Daar het spectrum van het zwarte lichaam van geen enkele andere parameter dan de temperatuur – in het bijzonder niet van de materiaaleigenschappen – afhangt, is het een voor talloze doeleinden nuttige referentiebron.
Naast de grote praktische betekenis van het zwarte lichaam, geldt de ontdekking van stralingswet van Planck in 1900 tegelijk als de start van de kwantummechanica, aangezien Planck ter verklaring van zijn aanvankelijk slechts empirisch gevonden vergelijking moest aannemen dat licht – en elektromagnetische straling in het algemeen – niet continu maar alleen discreet in zogenaamde kwanta wordt opgenomen en afgegeven.
Verder combineerde de stralingswet van Planck wetmatigheden die reeds voor zijn ontdekking deels empirisch en deels op grond van thermodynamische beschouwingen waren gevonden:
- De wet van Stefan-Boltzmann, die zegt dat het uitgestraalde vermogen van een zwart lichaam evenredig is met de vierde macht van de temperatuur.
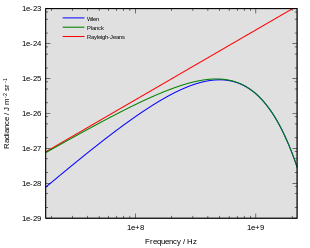
- De wet van Rayleigh-Jeans, die de spectrale energieverdeling bij lange golflengtes beschrijft.
- De stralingswet van Wien, die de spectrale energieverdeling bij korte golflengtes beschrijft.
- De verschuivingswet van Wien, in 1893 door Wilhelm Wien (1864-1928) geformuleerd, die het verband tussen het emissiemaximum van een zwart lichaam en zijn temperatuur beschrijft.
Afleiding en geschiedenis[bewerken | brontekst bewerken]
Als vereenvoudigd voorbeeld kan men uitgaan van een kubusvormige holle ruimte met ribbe L en volume L3, waarbinnen zich elektromagnetische straling in thermisch evenwicht bevindt. In deze evenwichtssituatie kunnen alleen staande golven optreden. De toegestane golven kunnen in willekeurige richtingen lopen, maar moeten daarbij wel voldoen aan de randvoorwaarde dat er tussen twee tegenover elkaar staande wanden steeds een geheel aantal halve golflengtes moet passen. Dit vanwege het feit dat er zich binnenin het wandmateriaal geen elektromagnetische golven kunnen bevinden, zodat op het oppervlak van de wanden de elektrische en magnetische veldsterkte nul moeten zijn. Op de wanden moeten de golven dus knopen hebben. Er zijn dus alleen bepaalde discrete trillingstoestanden toegestaan; de totale straling in de holle ruimte is dus samengesteld uit deze staande golven.
De toestandsdichtheid[bewerken | brontekst bewerken]
Het aantal toegestane trillingstoestanden neemt bij hogere frequentie toe, omdat er voor golven met kortere golflengte meer mogelijkheden zijn om zich zo in de ruimte in te passen dat alle x-, y- en z-componenten op elk oppervlak een knoop hebben. Het aantal toegestane trillingstoestanden in het frequentie-interval tussen v + dv en per volume-eenheid heet de toestandsdichtheid g(ν) dν en bedraagt:
De ultravioletcatastrofe[bewerken | brontekst bewerken]
Men kan elk van deze trillingstoestanden per frequentie-interval opvatten als een harmonische oscillator met frequentie ν. Als al deze oscillatoren in thermisch evenwicht bij een temperatuur T trillen, dan zou men volgens het equivalentieprincipe uit de klassieke thermodynamica verwachten dat elk van deze oscillatoren gemiddeld een kinetische energie kT/2 en een potentiële energie kT/2 heeft, dus in totaal kT. De energiedichtheid van de zwarte straling in het frequentie-interval tussen ν en ν + dν zou dus het product zijn van de toestandsdichtheid van de toegestane trillingstoestanden g(ν) dν en de gemiddelde energie per klassieke trillingstoestand kT, zodat
- .
Dit is de stralingswet van Rayleigh en Jeans. Deze geeft de gemeten energiedichtheid bij lage frequenties goed weer, maar voorspelt bij hogere frequenties een met toenemende frequentie kwadratisch stijgende energiedichtheid, zodat de holte over alle frequenties geïntegreerd een oneindig grote hoeveelheid energie zou moeten bevatten. Dit wordt wel de ultravioletcatastrofe genoemd.[2] Het probleem is dat elke aanwezige trillingstoestand weliswaar gemiddeld slechts de energie kT bevat, maar dat er oneindig veel van dergelijke trillingstoestanden geëxciteerd zijn.
De empirische oplossing[bewerken | brontekst bewerken]
Planck hanteerde bij het afleiden van zijn stralingswet niet de uitgangspunten van Rayleigh, maar ging uit van de entropie en voegde in de vergelijking proberenderwijs enkele termen toe die volgens de toenmalige natuurkundige inzichten weliswaar niet te begrijpen waren, maar er ook niet mee in tegenspraak waren. Heel eenvoudig was een extra term, die tot een formule leidde die de reeds gemeten spectra zeer goed beschreven (1900).[3] Daarmee bleef deze formule zuivere empirie, maar hij beschreef de bekende meetresultaten over het gehele frequentiespectrum correct. Maar Planck was daarmee niet tevreden. Hij slaagde erin de stralingsconstanten C en c uit de formule van Wien te vervangen door natuurconstanten; er bleef alleen een factor h („help”) over.
De kwantumhypothese[bewerken | brontekst bewerken]
Uitgaande van de verbeterde empirische stralingsformule, kwam Planck binnen enkele maanden tot een baanbrekend resultaat, dat het begin van de kwantummechanica zou worden: Hij moest, zelfs tegen zijn eigen overtuiging in, toegeven dat de energieafgifte niet continu plaatsvond, maar alleen in veelvouden van kleinste h-eenheden, die later naar hem de constante van Planck genoemd werd. Volgens deze door Planck ingevoerde kwantumhypothese kan een oscillator met frequentie ν niet willekeurige hoeveelheden energie opnemen of afgeven, maar alleen gehele veelvouden van de minimale energie hν. In het bijzonder heeft hij een minimale energie hν nodig om überhaupt te worden geëxciteerd. Trillingstoestanden waarvan de minimale energie hν duidelijk boven de thermisch beschikbare energie kT ligt, kunnen niet worden geëxciteerd, zij blijven bevroren. Trillingstoestanden waarvan de minimale energie hν slechts weinig boven kT ligt, kunnen met een bepaalde waarschijnlijkheid worden geëxciteerd, zodat een zekere fractie van hen aan de totale energie in de holte bijdraagt. Alleen trillingstoestanden met een lage minimale energie hν, dus met lage frequentie, kunnen de aangeboden thermische energie volledig opnemen en worden (gemiddeld) met zekerheid geëxciteerd.
Gekwantiseerde trillingstoestanden[bewerken | brontekst bewerken]
De statistische thermodynamica laat zien dat door toepassing van de kwantumhypothese en de Bose-Einsteinstatistiek een trillingstoestand met frequentie ν gemiddeld aan energie bevat:
Deze relatie betekent dat hogerfrequente elektromagnetische trillingstoestanden, die volgens de meetkundige criteria in de holte kunnen bestaan, vanwege hun hoge excitatiedrempel niet door de beschikbare thermische energie kunnen worden geëxciteerd en daardoor niet aan de energiedichtheid in de holte kunnen bijdragen.
De stralingswet[bewerken | brontekst bewerken]
Het product van de toestandsdichtheid van de toegestane trillingstoestanden g(ν) d(ν) en de gemiddelde energie per gekwantiseerde trillingstoestand E(ν, T) levert de energiedichtheid volgens Planck:
- .
Omdat de gemiddelde energie bij hoge frequenties sneller afneemt dan de toestandsdichtheid toeneemt, neemt de spectrale energiedichtheid – die immers hun product is – naar hogere frequenties weer af nadat hij een maximum heeft doorlopen, zodat de totale energie eindig blijft. Zo verklaarde Planck vanuit zijn kwamtumhypothese waarom de op grond van de klassieke thermodynamica voorspelde ultravioletcatastrofe in werkelijkheid niet optreedt.
Belangrijke toepassingen van de stralingswet[bewerken | brontekst bewerken]

De stralingswet van Planck wordt op verschillende manieren weergegeven, die grootheden voor intensiteiten, stroomdichtheden en spectrale verdelingen gebruiken die voor de te beschrijven situatie relevant zijn. Al deze verschillende vormen zijn slechts varianten van deze ene wet.
De eerste nevenstaande afbeelding toont de stralingsspectra volgens Planck voor temperaturen tussen 300 K en 1000 K op een lineaire schaal. Men herkent de typische klokvorm met een duidelijk maximum, een steile daling naar de korte golflengten en een langzame daling naar de langere golflengten. De ligging van het maximum verschuift bij toenemende temperatuur naar de kortere golflengtes, conform de verschuivingswet van Wien. Tegelijk neemt, volgens de wet van Stefan-Boltzmann, de totale uitstraling toe met de vierde macht van de temperatuur. Door deze sterke toename van de stralingsintensiteit bij stijgende temperatuur is het moeilijk, curves voor een groot temperatuurbereik in één diagram weer te geven.

De tweede afbeelding heeft daarom langs beide assen een logaritmische schaal. Getoond worden de spectra voor temperaturen tussen 100 K en 10.000 K.
De curve voor 300 K is rood weergegeven; dit komt overeen met typische omgevingstemperaturen. Het maximum van deze curve ligt bij 10 μm; in dit golflengtegebied, het langgolvig infrarood, vindt dan ook de stralingsuitwisseling plaats van voorwerpen op kamertemperatuur. Typische infraroodthermometers en thermografiecamera’s werken in dit gebied.
De curve voor 3000 K komt overeen met het typische stralingsspectrum van een gloeilamp. Hierbij wordt reeds een deel van de straling in het zichtbare deel van het spectrum uitgezonden. Het maximum ligt echter nog in het nabije infrarood.
Geel weergegeven is de curve voor 5777 K, de gemiddelde temperatuur van de zon. Het stralingsmaximum ligt nu midden in het zichtbare deel van het spectrum.
Veelgebruikte formules en eenheden[bewerken | brontekst bewerken]
Voor de wiskundige voorstelling van de wet van Planck bestaan er talloze varianten, afhankelijk van de vraag of de wet als functie van de frequentie of van de golflengte moet worden geformuleerd, of de stralingsintensiteit in een bepaalde richting of de uitstraling in alle richtingen moet worden beschreven, of de stralingsgrootheden, energiedichtheden dan wel aantallen fotonen moeten worden beschreven.
Vaak gebruikt men de formule voor de specifieke spectrale uitstraling van een zwart lichaam met absolute temperatuur
in frequentievorm:
- (SI-eenheid W m−2 Hz−1)
en in golflengtevorm:
- (SI-eenheid W m−2 m−1)
De grootheid is het stralingsvermogen dat door een oppervlakte-element dA in het frequentiebereik tussen ν en ν + dν in de volledige halvebolruimte wordt uitgestraald. Verder is h de constante van Planck, c de lichtsnelheid en k de constante van Boltzmann.
Bij het omrekenen van de frequentievorm naar de golflengtevorm en terug dient er rekening mee te worden gehouden dat vanwege
geldt
- en .
Zie ook[bewerken | brontekst bewerken]
Externe links[bewerken | brontekst bewerken]
Noten[bewerken | brontekst bewerken]
- ↑ M. Planck: Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum, Verhandlungen der Deutschen physikalischen Gesellschaft 2 (1900) Nr. 17, p. 245; Berlijn, 14 december 1900) (Engelse vertaling)
- ↑ In tegenstelling tot wat vaak wordt beweerd, hebben de wet van Rayleigh-Jeans en de ultravioletcatastrofe geen rol gespeeld bij Plancks ontdekking van zijn stralingswet. De fysisch onzinnige divergentie van de wet van Rayleigh-Jeans bij hoge stralingsfrequenties werd voor het eerst in januari 1905 onafhankelijk van elkaar door Einstein, Rayleigh en Jeans beschreven. Het begrip ultravioletcatastrofe werd voor het eerst in 1911 gebruikt door Paul Ehrenfest (Ehrenfest, P: “Welche Züge der Lichtquantenhypothese spielen in der Theorie der Wärmestrahlung eine wesentliche Rolle?” Annalen der Physik, vol. 341, issue 11 (1911), 91–118.
- ↑ Giulini, D en N. Straumann, N.: „… ich dachte mir nicht viel dabei …” Plancks ungerader Weg zur Strahlungsformel, Oktober 2000 arXiv:quant-ph/0010008












