Atoommodel van Bohr
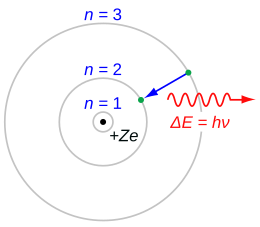
Een elektron (groen balletje hier) springt vanuit een hogere baan (n=3) rond de atoomkern (zwart balletje) naar een lagere baan (n=2). Vanwege behoud van energie wordt het energieverschil ΔE van het elektron in de twee banen uitgezonden als elektromagnetische straling, bijvoorbeeld licht (hier in rood weergegeven). De uitgezonden energie wordt volgens Planck geschreven als de constante van Planck (h) maal de frequentie (ν, bij licht de kleur) van de uitgezonden straling.
Het atoommodel van Bohr is een in 1913 door Niels Bohr geïntroduceerde theorie die de opbouw van atomen beschrijft. Bohr modificeerde het atoommodel van Rutherford door het invoeren van kwantiseringen, gebaseerd op de theorie van Planck over de kwantisering van straling. Het model van Bohr is daarmee het eerste model met kwantumtheoretische aspecten. Voor zijn theorie kreeg Bohr in 1922 de Nobelprijs voor Natuurkunde.
In het atoommodel van Rutherford cirkelen de lichte elektronen als een wolk om een positief geladen zware kern. In de klassieke natuurkunde zenden bewegende ladingen echter elektromagnetische straling uit, zodat het atoom niet stabiel zou zijn. Om aan dit probleem te ontkomen, postuleerde Bohr simpelweg dat de elektronen zich alleen in banen kunnen bevinden op specifieke afstanden van de kern, en dat een elektron in zo'n baan geen straling uitzendt.
Geschiedenis
In 1913 publiceerde Niels Bohr in het Philosophical Magazine in juli, september en november drie artikelen met de gemeenschappelijke titel "On the Constitution of Atoms and Molecules’’. Het eerste artikel[1] ging over het waterstofatoom, het tweede[2] over willekeurige atomen, en het derde over de structuur van moleculen. Hij baseerde zijn werk op ideeën van Max Planck uit 1900 over kwantisering om een oplossing te vinden voor de stabiliteit van atomen. Zijn theorie gaf een redelijk adequate beschrijving van de eenvoudigste configuraties, zoals het waterstofatoom en het heliumion, maar schoot tekort voor complexere structuren, zelfs al voor het waterstofmolecuul en het heliumatoom. De tekortkomingen van het model van Bohr zouden later door de kwantummechanica worden opgeheven.
De kern van Bohrs Nobellezing in 1922 in de Zweedse Academie der Wetenschappen was een tweetal postulaten:
- Among the conceivably possible states of motion in an atomic system there exist a number of so-called stationary states which, in spite of the fact that the motion of the particles in these states obeys the laws of classical mechanics to a considerable extent, possess a peculiar, mechanically unexplainable stability, of such a sort that every permanent change in the motion of the system must consist in a complete transition from one stationary state to another.
(Onder de denkbaar mogelijke toestanden van beweging in een atomair systeem is er een aantal zogeheten stationaire toestanden die, ondanks het feit dat de beweging van de deeltjes in deze gebieden in hoge mate gehoorzaamt aan de wetten van de klassieke mechanica, een bijzondere, mechanisch onverklaarbare stabiliteit bezitten, zodanig dat elke blijvende verandering in de beweging van het systeem moet bestaan uit een volledige overgang van de ene stationaire toestand in de andere.)
- While in contradiction to the classical electromagnetic theory no radiation takes place from the atom in the stationary states themselves, a process of transition between two stationary states can be accompanied by the emission of electromagnetic radiation, which will have the same properties as that which would be sent out according to the classical theory from an electrified particle executing an harmonic vibration with constant frequency. This frequency has, however, no simple relation to the motion of the particles of the atom, but is given by the relation = E' - E", where h is Planck’s constant, and E' and E" are the values of the energy of the atom in the two stationary states that form the initial and final state of the radiation process. Conversely, irradiation of the atom with electromagnetic waves of this frequency can lead to an absorption process,whereby the atom is transformed back from the latter stationary state to the former.
(Terwijl in tegenstelling tot de klassieke elektromagnetische theorie geen straling plaatsvindt van het atoom in de stationaire toestanden zelf, kan een proces van overgang tussen twee stationaire toestanden gepaard gaan met het uitzenden van elektromagnetische straling, die dezelfde eigenschappen zal hebben als die die zou worden uitgezonden volgens de klassieke theorie van een elektrisch geladen deeltje dat een harmonische trilling uitvoert met constante frequentie. Deze frequentie heeft echter geen eenvoudig verband met de beweging van de deeltjes van het atoom, maar wordt gegeven door de relatie = E - E", waarin h de constante van Planck is, en E en E" de waarden zijn van de energie van het atoom in de beide stationaire toestanden die de begin- en eindtoestand vormen van het stralingsproces. Omgekeerd kan bestraling van het atoom met elektromagnetische golven van deze frequentie leiden tot een absorptieproces, waarbij het atoom teruggetransformeerd wordt uit de laatstgenoemde stationaire toestand naar de eerste.)
Het atoommodel
Het atoommodel van Bohr was gebaseerd op het atoommodel van Rutherford, waarin zeer lichte elektronen zich in cirkelvormig banen rondom een kleine, positief geladen zware kern bewegen. Om de tekortkomingen van dit model op te heffen formuleerde Bohr eenvoudigweg enkele postulaten.
De genoemde postulaten kunnen als volgt nader gespecificeerd worden:
- Elektronen in een atoom bewegen onder invloed van de wet van Coulomb rond de kern in cirkelvormige banen.
- Van deze banen is slechts een discreet aantal toegelaten, op specifieke afstanden van de kern. Deze banen, die stationaire toestanden genoemd worden, houden verband met bepaalde hoeveelheden energie. Daarom heten de stationaire toestanden ook energieschillen of energieniveaus.
- In een stationaire toestand bewegen de elektronen zonder straling op te wekken, dus zonder energieverlies.
- Een elektron kan alleen van de ene stationaire toestand overgaan in een andere stationaire toestand. Zo'n overgang heet kwantumsprong en ligt buiten het geldigheidsbereik van de klassieke mechanica en elektrodynamica.
- Bij een kwantumsprong van een toestand met energieniveau naar een andere toestand met energieniveau wint of verliest het elektron energie. Het energieverschil tussen de banen wordt als het positief is uitgezonden als een foton, en als het negatief is geleverd door de absorptie van een foton. De frequentie van het foton wordt volgens Planck bepaald door , waarin de constante van Planck is.
- Als het elektron in de begintoestand slechts langzaam beweegt en naar de energetisch naastgelegen toestand springt, is de frequentie van de uitgezonden of geabsorbeerde straling bij benadering gelijk aan de omloopfrequentie van het elektron, zoals in de klassieke theorie.
Schillen
Volgens het atoommodel van Bohr houden de elektronen van een atoom zich op in een aantal schillen rondom de kern, die een verschillend energieniveau hebben. Elke schil kan een beperkt aantal elektronen bevatten. De elektronen van een stabiel atoom zitten in de schillen met de laagst mogelijke energie.
Schillen worden met toenemende afstand tot de kern aangeduid door de letters K, L, M, N, O, P en Q. Bohr begon te tellen bij K, omdat hij het voor mogelijk hield dat er nog schillen tussen K en de kern zouden zijn. Het rangnummer wordt het schilnummer n genoemd. Een schil met rangnummer n kan maximaal 2n2 elektronen bevatten, zoals aangegeven in de onderstaande tabel.[3]
Schil K L M N O P Q Nummer (n) 1 2 3 4 5 6 7 Max. bezetting 2 8 18 32 50 72 98
Een natriumatoom bijvoorbeeld heeft elf elektronen. In de stabiele toestand zitten er dus 2 elektronen in de K-schil, 8 in de L-schil en het laatste elektron zit in de M-schil.
Energie-emissie door een waterstofatoom
Uit Bohrs laatste postulaat blijkt wat er gebeurt als een atoom energie opneemt (bijvoorbeeld door verhitting): het elektron dat zich voor de verhitting in zijn grondtoestand bevindt (toestand met de laagste energie-inhoud) kan dan naar een hogere baan springen (van energieniveau 1 naar energieniveau 2). Deze aangeslagen toestand is echter niet stabiel waardoor het elektron terugvalt naar een lager gelegen baan. De overtollige energie is het energieverschil tussen beide energieniveaus en wordt terug uitgestraald in de vorm van elektromagnetische straling.
Bij analyse van dit licht door een prisma blijkt het (in tegenstelling tot zonlicht) uit een discreet lijnenspectrum te bestaan. Dit lijnenspectrum bestaat uit een reeks lijnen bij een beperkt aantal golflengten. Op de andere golflengten worden geen lichtdeeltjes uitgestraald. Zo ontstaat er voor elk atoom een specifiek lijnenspectrum, met een beperkt aantal uitgestraalde golflengten. Bevinden deze golflengten zich tussen de 350 en 700 nm, dan is het licht zichtbaar voor het menselijk oog.
Theoretisch zijn deze bevindingen een gevolg van de relatie tussen de energie en de golflengte. De energie nodig om een golf uit te zenden met frequentie kan men vinden via de relatie
Hierin is E de energie (in dit geval het energieverschil tussen energieniveau 2 en energieniveau 1) en de frequentie van de uitgezonden golf. ℎ is de constante van Planck, gelijk aan
Deze relatie komt voort uit de deeltje-golfdualiteit en levert ook een directe link tussen de energie E en de golflengte λ, aangezien de snelheid van de uitgezonden straling gelijk is aan de lichtsnelheid, gegeven door
Energieniveaus
Als er energie aan een atoom wordt toegevoegd, bijvoorbeeld doordat de stof verhit wordt, kunnen er elektronen naar een hogere energietoestand gaan. Dit heet een aangeslagen toestand. Het overgaan naar een hogere energietoestand heet excitatie. Het atoom is dan niet meer in de stabiele toestand.
Als er een elektron terugvalt naar een lager energieniveau, zendt het atoom energie uit in de vorm van elektromagnetische straling, bijvoorbeeld in de vorm van licht. Dat heet emissie van stralingsenergie.
De stralingsenergie die vrijkomt bij een bepaalde elektronensprong komt overeen met het energieverschil tussen deze energieniveaus. De waarden van de sprongen zijn typisch voor elk chemisch element. De stralingsenergie bepaalt de golflengte van de straling, en dus de kleur van het uitgestraalde licht.
Experimentele basis
Lichtuitstraling
Niels Bohr stelde vast dat metalen bij verhitting in een vlam of bij toevoer van energie een typische lichtkleur voor dat element vertonen. Bij natrium is dit geel, bij calcium baksteenrood en bij koper is dit groen. In het dagelijkse leven zien we deze kleuren vaak terug. Langs veel autowegen (opvallend in België) staat autowegverlichting die inderdaad geel-oranje-achtig is omdat het om natriumdamp-lampen gaat.
Emissiespectrum
De straling die door enkelvoudige stoffen wordt uitgezonden, kan verder ontleed worden als je de straling door een prisma heen stuurt. Als het licht van een gloeiend hete zuivere stof via een prisma op een wit vlak valt, vertonen zich lijntjes met verschillende kleuren. Dat heet het emissiespectrum. Elk lijntje komt overeen met een bepaalde energie, en dus met een bepaalde overgang tussen twee elektronenschillen. Zo geeft een elektron uit een natriumatoom dat terugvalt van de N-schil naar de M-schil, de bekende gele kleur die natriumlampen uitstralen.
Door de uitgestraalde energieën van een groot aantal elementen te analyseren, kon Bohr afleiden welke energieniveaus in een element voor konden komen.
Nadat de emissiespectra van een groot aantal elementen waren bepaald, konden deze ook worden gebruikt om de samenstelling van stoffen te bepalen met behulp van atomaire-emissiespectrometrie.
Verdere verfijningen
- Het atoommodel van Sommerfeld (1916)
- De magnetische niveaus
- De spin van een elektron (1922)
- Het golfmechanisch atoommodel (De Broglie, Schrödinger en Heisenberg, 1927)
Zie ook
- ↑ http://web.ihep.su/dbserv/compas/src/bohr13/eng.pdf
- ↑ http://web.ihep.su/dbserv/compas/src/bohr13b/eng.pdf
- ↑ Shell atomic model, Encyclopaedia Britannica, geraadpleegd op 2 juni 2018










