Fonon
In de natuurkunde is een fonon een kwantum energie in trillingen die voorkomen in periodieke rangschikkingen van atomen of moleculen. Een fonon is een elastische golf die een aangeslagen toestand in een vaste of vloeibare stof aanduidt.
In de studie van de fysica van de gecondenseerde materie doet men onder meer onderzoek naar fononen; vooral met betrekking tot de warmtegeleiding en elektriciteit spelen fononen een belangrijke rol.
Fononen zijn verantwoordelijk voor de verplaatsing van warmte en geluid door een medium. Fononen van lage frequentie zijn in veel gevallen verantwoordelijk voor geluidsverplaatsing, terwijl fononen van hoge frequentie meestal verantwoordelijk zijn voor de verplaatsing van warmte.
Definitie[bewerken | brontekst bewerken]
Een fonon is een gekwantiseerde collectieve trillingswijze van een kristal. De energie van trillingen in roosters is gekwantiseerd; een kwantum van dergelijke energie wordt een fonon genoemd.
Algemeen[bewerken | brontekst bewerken]
In een kristallijn materiaal zijn de atomen en/of moleculen via wisselwerkingen van wisselende sterkte aan elkaar gekoppeld. In sommige structuren, zoals in diamant, zijn dit sterke covalente bindingen, in andere zoals vast argon (bij lage temperatuur) zijn het slechts zwakke vanderwaalswisselwerkingen. De meeste materialen nemen een tussenpositie in.
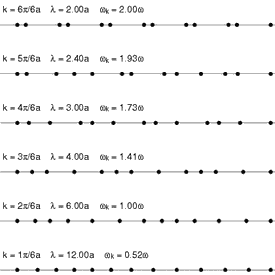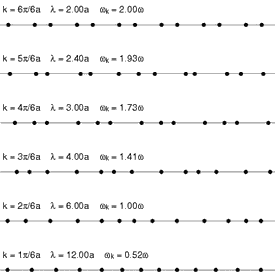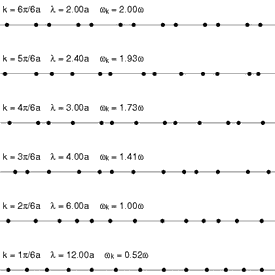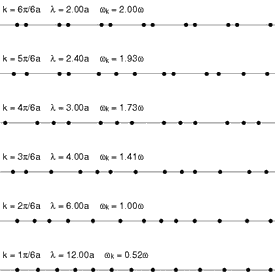
In een los molecuul kan men vaak de trillingswijzen van de afzonderlijke bindingen in eerste instantie als een harmonische oscillator beschrijven. Bij grotere moleculen ontstaan er echter trillingswijzen die meerdere atomen en hun bindingen omvatten. Bij een vaste stof moet men in de regel alle atomen van het gehele kristal in hun geheel beschouwen. De natuurlijke trillingswijzen van zo'n systeem kunnen dan het beste in termen van Bloch-functies (sinusoïdale golven) beschreven worden. De golven worden gekenmerkt door een golfvector k in een beschrijving die analoog is aan die van de elektronenbanden van het kristal.
De energie van de trilling E(k) is een functie van k en men kan deze functie als een band van trillingswijzen beschouwen. Omdat er meestal meer dan één atoom in een eenheidscel van de structuur zit, zijn er in het algemeen voor iedere waarde van de golfvector een aantal verschillende trillingswijzen met verschillende symmetrie.
Een fonon is een boson, een deeltje met geheel spingetal (0, ±1, ±2, …), net als bijvoorbeeld het Higgsdeeltje. In tegenstelling tot fermionen vallen bosonen niet onder het uitsluitingsprincipe van Pauli, waardoor dus meerdere fononen zich in dezelfde toestand kunnen bevinden. Voor fermionen geldt dat slechts één deeltje zich in een specifieke toestand kan bevinden.
Iedere trillingswijze kan afzonderlijk als een gekwantiseerd systeem beschouwd worden. Zo'n kwantum wordt fonon genoemd. Doordat fononen bosonen zijn, kan een bepaalde trillingswijze meer dan een keer tegelijk aangeslagen worden.
De fononen beïnvloeden energie van de stof van het rooster waarin ze zich bevinden door middel van de ook voor fotonen bekende formule:
Waarin ε de energie is, ω de frequentie van de golf, n het gehele aantal fononen.
De energie van een fonon is discreet verdeeld, dit wil zeggen dat de energie van fononen niet via een continue verdeling verhoogd kan worden, maar dat dit stapsgewijs gaat. Er bestaan dus geen halve fononen, alleen gehele fononen.[1]
Fononen en fotonen zijn zeer vergelijkbaar. Het zijn allebei massaloze deeltjes, maar beide hebben wel een impuls en een frequentie.
Een fonon heeft de eigenschappen van een golf, maar bevat opvallend genoeg ook de eigenschappen van een deeltje. Een fonon heeft een transversale of longitudinale golfbeweging en is massaloos. Echter kan een fonongolf ook gezien worden als een stroom van deeltjes. Een fonon heeft zowel een frequentie als een impuls. De combinatie van eigenschappen van zowel een golf als een deeltje wordt de dualiteit van golven en deeltjes genoemd. Een fonon kan, net als een foton, worden gezien als een gekwantiseerde golf en als een deeltje. Net als fotonen zijn fononen ook bosonen. Echter in tegenstelling tot fotonen kunnen fononen van verschillende golflengtes wel met elkaar interacteren.
Geschiedenis[bewerken | brontekst bewerken]

Net als het vakgebied van gecondenseerde materie is het begrip fonon in de natuurkunde nog relatief jong. Het fonon werd voor het eerst geïntroduceerd door de Russisch-Duitse natuurkundige Igor Tamm in een artikel uit 1930. In het artikel van Tamm werd het woord fonon echter nog niet genoemd. Die naam kreeg het pas later in 1932 dankzij de Russische natuurkundige Yakov Frenkel, die in een artikel doorborduurde op het werk van Tamm. Het woord fonon is afkomstig van het Griekse φωνή (phonē), wat geluid of stem betekent.[2]
Kristalimpuls[bewerken | brontekst bewerken]
Vanwege de golf/deeltje-dualiteit van het karakter van fononen behandelt men een fonon alsof het een impuls betreft met golfvector . De golfvector is echter periodiek met periode:
waarin de eenheidsvector in het kristalrooster is en het aantal eenheidsvectoren.[3]
Hierdoor hoeft de golfvector alleen bepaald te worden voor de (eerste) Brillouinzone. Echter het bepalen van de impuls van een fonon kan strikt genomen niet door middel van de golfvector, omdat hetzelfde fonon wordt beschreven met de impuls als . Aan fononen is daarom het zogenaamde kristalmomentum of quasimomentum toegekend, wat de impuls van een fonon in de (eerste) Brillouinzone betreft.[4]
De kristalimpuls is een erg nuttige grootheid voor het rekenen met fononen. Wanneer twee of meer fononen met elkaar botsen, zijn zowel de energie als de kristalimpuls behouden. Dit is belangrijk in de studie van de gecondenseerde materie omdat de impuls van een fonon niet behouden is tijdens de botsingen tussen fononen, maar de kristalimpuls dus wel.
Akoestische en optische fononen[bewerken | brontekst bewerken]

De dispersierelatie:
waarmee de eigenschappen van een golf in het medium bepaald kunnen worden, geeft voor een stof met twee of meer atomen, twee of meer vertakkingen. Het aantal vertakkingen is afhankelijk van het aantal vrijheidsgraden van de atomen. Deze vertakkingen worden de optische tak en akoestische tak genoemd. De akoestische tak is de onderste van de vertakkingen, als er twee vertakkingen zijn. Wanneer er meer dan twee vertakkingen in de dispersieplot zichtbaar zijn, dan is de onderste helft takken akoestisch en de bovenste helft optisch. De snelheid van voortplanting van een akoestisch fonon is gelijk aan de helling van de akoestische tak van de dispersierelatie en gelijk aan de voortplantingssnelheid van geluid in het betrokken medium. Akoestische fononen geven de verplaatsingen weer van atomen buiten hun roosterpositie. De beweging van de atomen is in fase met andere atomen en kan zowel een longitudinale golf zijn als een transversale golf. Akoestische fononen zijn laagfrequente fononen en daarom vooral verantwoordelijk voor de verplaatsing van geluid in een medium. De groepssnelheid van de fononen is gelijk aan de snelheid van geluid in het medium.
De optische fononen geven atomen weer die met elkaar uit fase bewegen. In het geval van een longitudinale golf betekent dat dat het ene atoom tegengesteld beweegt ten opzichte van het naaste atoom. Optische fononen komen alleen voor als de roosterbasis van een kristal bestaat uit twee of meer verschillende atomen. Optische fononen kunnen in tegenstelling tot akoestische fononen met fotonen interageren en zo energie opnemen. Vanwege het gekwantiseerde karakter van het fonon brengt de opname van een foton met voldoende energie een fonon naar een hogere energietoestand. Als het fonon zich nog in de grondtoestand bevindt, kan de interactie met een foton dit fonon in een aangeslagen toestand brengen. Ook bij optische fononen kunnen, net als bij akoestische fononen, de golven zowel longitudinaal als transversaal zijn. Optische fononen zijn hoogfrequente fononen en zo vooral verantwoordelijk voor de verplaatsing van warmte in een medium.
Bronnen, noten en/of referenties
|








