Kleurlading

In de deeltjesfysica is kleurlading een eigenschap van quarks en gluonen, die gerelateerd is aan de sterke wisselwerking van de deeltjes in de theorie van kwantumchromodynamica (QCD). Kleurlading heeft analogieën met de notie van elektrische lading van de deeltjes, maar vanwege de wiskundige complicaties van QCD zijn er veel technische verschillen. De "kleur" van quarks en gluonen staat volledig los van visuele perceptie van kleur. Het is een grillig gekozen naam voor een eigenschap die zich bijna niet manifesteert bij afstanden boven de grootte van een atoomkern. De term kleur werd gekozen omdat de abstracte eigenschap, waaraan deze term refereert, betrekking heeft op drie aspecten, dit naar analogie met de drie primaire kleuren rood, groen en blauw. Ter vergelijking: elektromagnetische lading heeft één enkel aspect, dat de waarden positief of negatief kan aannemen.

In 1964, kort nadat het bestaan van quarks voor het eerst werd voorgesteld, introduceerde Oscar Greenberg het begrip "kleurlading" om uit te leggen hoe quarks binnen een aantal hadronen in verder identieke kwantummechanische toestanden naast elkaar kunnen bestaan zonder het uitsluitingsprincipe van Pauli te overtreden. Het concept bleek nuttig te zijn. De theorie van de kwantumchromodynamica is sinds de jaren 1970 in ontwikkeling en vormt een belangrijk onderdeel van het standaardmodel van de deeltjesfysica.

Rood, groen en blauw

In de QCD kan de kleur van een quark drie waarden hebben, die respectievelijk rood, groen en blauw worden genoemd. De kleur van een antiquark kan ook drie waarden aannemen, die respectievelijk antirood, antigroen en antiblauw worden genoemd. Deze drie antikleuren worden hier respectievelijk voorgesteld als cyaan, magenta en geel. Gluonen zijn mengsels van twee kleuren, zoals rood en antigroen. Zo'n mengsel noemt men de kleurlading van het gluon. In de QCD beschouwt men acht gluonen van de negen kleur-antikleurcombinaties als uniek.

Het volgende voorbeeld illustreert de koppelingsconstanten voor kleurgeladen deeltjes:

• 
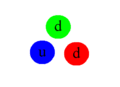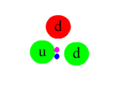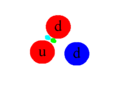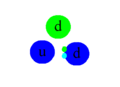
  De quarkkleuren (rood, groen, blauw) combineren tot kleurloos.
• 
  De quarkantikleuren (antirood, antigroen en antiblauw) combineren ook tot kleurloos.

• 
  Een hadron met drie quarks (rood, groen, blauw) vóór een kleurverandering.
• 
  Een rode quark straalt een rood-antigroen gluon uit en wordt daardoor groen.
• 
  Een groene quark heeft de rood-antigroene gluon geabsorbeerd en wordt nu rood; de kleur is bewaard.
• 
  Een animatie van de interactie binnen een neutron

Koppelingsconstante en lading

In een kwantumveldentheorie zijn een koppelingsconstante en een lading verschillende maar verwante begrippen. De koppelingconstante stelt de grootte van de interactiekracht voor; in de kwantumelektrodynamica is de fijnstructuurconstante bijvoorbeeld een koppelingsconstante. De lading in een ijktheorie heeft te maken met de manier, waarop een deeltje zich onder de ijksymmetrie in een ander deeltje transformeert; dat wil zeggen haar representatie onder de ijkgroep. Het elektron heeft bijvoorbeeld een lading −1 en het positron heeft lading +1, hetgeen impliceert dat de ijktransformatie in zekere zin tegengestelde effecten op hen heeft. Als men in een specifiek geval een lokale ijktransformatie φ(x) toepast in de elektrodynamica, dan vindt men

$A_{\mu }\to A_{\mu }+\partial _{\mu }\phi (x)$,   $\psi \to \exp[iQ\phi (x)]\psi$  and  ${\overline {\psi }}\to \exp[-iQ\phi (x)]{\overline {\psi }}$

waar $A_{\mu }$ het foton- en $\psi$ het elektron veld met $Q=-1$ is (een streepje boven $\psi$ duidt haar antideeltje - het positron - aan). Aangezien de QCD een niet-abelse theorie is, zijn de representaties, en dus de kleurladingen, ingewikkelder. Zij worden in de volgende paragraaf behandeld.

Quark- en gluonvelden en kleurladingen

In de QCD is de ijkgroep de niet-Abelse groep SU(3). De draaiende koppeling wordt meestal aangeduid met α_s. Elke smaak van quark behoort tot de fundamentele representatie (3) en bevat een drietal velden die samen worden aangeduid met ψ. Het antiquarkveld behoort tot de complex geconjugeerde representatie (3^*) en bevat ook een drietal velden. Men kan schrijven

$\psi ={\begin{pmatrix}\psi _{1}\\\psi _{2}\\\psi _{3}\end{pmatrix}}$  en  ${\overline {\psi }}={\begin{pmatrix}{\overline {\psi }}_{1}^{*}\\{\overline {\psi }}_{2}^{*}\\{\overline {\psi }}_{3}^{*}\end{pmatrix}}.$

Het gluon bevat een octet van velden, behoort tot de geadjungeerde representatie (8), en kan door van Gell-Mann-matrices gebruik te maken worden geschreven als

${\mathbf {A} }_{\mu }=A_{\mu }^{a}\lambda _{a}.$

Alle andere deeltjes behoren tot de triviale representatie (1) van kleur SU(3). De kleurlading van elk van deze velden wordt volledig gespecificeerd door de representaties. Quarks hebben een kleurlading van rood, groen of blauw en antiquarks hebben een kleurlading van antirood, antigroen of antiblauw. Gluonen hebben een combinatie van twee kleurladingen (een van rood, groen of blauw en een van antirood, antigroen en antiblauw) in een superpositie van toestanden, die worden gegeven door de Gell-Mann-matrices. Alle andere deeltjes hebben nul kleurlading. Wiskundig gesproken is de kleurlading van een deeltje de waarde van een bepaalde kwadratische Casimir-operator in de representatie van het deeltje.

In de eenvoudige taal, die hierboven werd geïntroduceerd, worden de drie indices "1", "2" en "3" in het kwarktriplet hierboven doorgaans geïdentificeerd met de drie kleuren. De kleurrijke taal mist echter het volgende punt. Een ijktransformatie in kleur SU(3) kan worden geschreven als ψ → Uψ, waar U een 3x3 matrix is, die behoort tot de groep SU(3). Dus na ijktransformatie zijn de nieuwe kleuren lineaire combinaties van de oude kleuren. In het kort; de vereenvoudigde taal, die hierboven is geïntroduceerd, is niet ijkvariant.

Kleurlading wordt behouden, maar de hierbij betrokken boekhouding is ingewikkelder dan alleen het optellen van ladingen, zoals gebeurt in de kwantumelektrodynamica. Een eenvoudige manier om dit te doen is om met eeninteractie vertexblik naar de QCD te kijken en deze te vervangen door een kleurlijnrepresentatie. De betekenis is de volgende. Laat ψ_i de i-e component van quarkveld representeert (losjes de i-e kleur genoemd). De kleur van een gluon wordt eveneens gegeven door a die correspondeert met de specifieke Gell-Mann-matrix waaraan het gluon is geassocieerd. Deze matrix heeft indices i en j. Dit zijn de kleurlabels van het gluon. Op de interactie vertex geeft men dit weer door q_i→_ij + q_j. De kleurlijn representatie volgt deze indices. Behoud van kleurlading betekent dat de uiteinden van deze kleurlijnen, hetzij in de begin-, hetzij in de eindstaat moeten zijn, of op gelijkwaardige wijze dat geen van deze lijnen in het midden van een diagram breken.

Aangezien gluonen kleurlading dragen, kunnen twee gluonen ook op elkaar inwerken. Een typische interactievertex (die de drie-gluonvertex wordt genoemd) voor gluonen is bijvoorbeeld g+g → g. Dat wordt hier getoond samen met haar kleurlijnrepresentatie. De kleurlijndiagrammen kunnen in termen van behoudswetten van kleur worden hergeformuleerd; dit is echter, zoals hierboven al eerder opgemerkt, geen ijkinvariante taal. Merk op dat in een typische niet-Abelse ijktheorie de ijkbosonen de lading van de theorie dragen, en dus ook wisselwerkingen van dit type kent; het W-boson in de elektrozwakke wisselwerking bijvoorbeeld. In de elektrozwakke theorie draagt de W-boson ook de elektrische lading, en interageert dus met een foton.

Zie ook

• Kleuropsluiting

Referenties

• (en) J. Richard Christman Color and Charm, 2001, Project PHYSNET document MISN-0-283.