Binomium van Newton

Het binomium van Newton is een wiskundige formule waarmee de macht van de som van twee grootheden kan worden uitgedrukt in een som van termen waarin de machten van de grootheden afzonderlijk voorkomen.

Natuurlijke exponent[bewerken | brontekst bewerken]

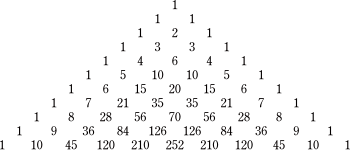
De eenvoudigste vorm is

(x+y)^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}y^{k}

waarbij $n$ een natuurlijk getal is, en de getallen

{n \choose k}={\frac {n!}{k!(n-k)!}}

de binomiaalcoëfficiënten.

Dit zijn de uitwerkingen voor $n=2,\ n=3$ en $n=4$ :

(x+y)^{2}=x^{2}+2xy+y^{2}

(x+y)^{3}=x^{3}+3x^{2}y+3xy^{2}+y^{3}

(x+y)^{4}=x^{4}+4x^{3}y+6x^{2}y^{2}+4xy^{3}+y^{4}

De binomiaalformule geldt voor alle reële en complexe getallen $x$ en $y$ , en meer in het algemeen voor elk paar elementen $x$ en $y$ in een commutatieve ring.

De coëfficiënten in het rechterlid van deze producten kunnen in een driehoek onder elkaar worden gezet, omdat er in ieder volgend product een product meer staat. Deze formule, en de rangschikking van binomiale coëfficiënten in een driehoek, worden vaak toegeschreven aan Blaise Pascal omdat die ze in de 17e eeuw beschreef. De formule was bij Chinese wiskundigen echter lang daarvoor al bekend.

Algemene formule[bewerken | brontekst bewerken]

Isaac Newton generaliseerde de formule voor andere exponenten tot

(1+x)^{z}=\sum _{k=0}^{\infty }{z \choose k}x^{k}

waarin $z$ een willekeurig complex getal kan zijn (dus ook elk reëel getal; niet noodzakelijkerwijs positief of geheel). De coëfficiënten van de reeks in het rechterlid zijn gedefinieerd door:

{z \choose k}={\frac {z(z-1)(z-2)\ldots (z-k+1)}{k!}}

,

met de afspraak dat

{z \choose 0}=1

De convergentiestraal van de reeks is 1, dat wil zeggen dat de reeks convergeert voor reële of complexe getallen met $|x|<1$ .

De formule is ook geldig in een Banach-algebra mits $\|x\|<1$ .

Het belangrijkste verschil tussen het gebruik van natuurlijke machten en complexe machten is dat bij het ontwikkelen van de reeks bij natuurlijke macht $n$ de binomiaal coëfficiënten 0 worden na $n+1$ termen. Daarom worden bij formule (1) slechts de eerste $n+1$ termen genomen. Illustratie van dit fenomeen:

{3 \choose 6}={\frac {3\cdot 2\cdot 1\cdot 0\cdot (-1)\cdot (-2)}{6!}}=0

In het algemene geval zorgt de factor 0 in de teller van deze breuk ervoor dat de binomiaalcoëfficiënten ${\tbinom {n}{k}}$ voor natuurlijke $n$ en $k$ gelijk zijn aan 0 als $n<k$ .

In het Engels wordt Newtons naam overigens slechts verbonden aan de algemene formule (Newton's generalised binomial theorem). Formule (1) heet simpelweg binomial theorem (binomiaalstelling).

Voor twee complexe getallen $x$ en $y$ met $|x|<|y|$ geldt:

(x+y)^{z}=y^{z}\left(1+{\frac {x}{y}}\right)^{z}=y^{z}\sum _{k=0}^{\infty }{z \choose k}\left({\frac {x}{y}}\right)^{k}=\sum _{k=0}^{\infty }{z \choose k}x^{k}y^{z-k}

Zie ook[bewerken | brontekst bewerken]

Zie de categorie Binomial theorem van Wikimedia Commons voor mediabestanden over dit onderwerp.