Kogelbaan

Verschillende kogelbanen onder een elevatie (afvuurhoek) van 70°, zonder en met laminaire stromingsweerstanden:
zwarte lijn: paraboolbaan zonder weerstand,
blauwe lijn: weerstand volgens de Wet van Stokes,
groene lijn: weerstand in een Newtonse vloeistof.

Een kleine bal stuitert op een harde ondergrond. De foto is gemaakt met een stroboscoop bij 25 flitsen per seconde. Bij elke botsing wordt de bal kortstondig afgeplat. Afplatting, luchtweerstand en draaiing zorgen ervoor dat de baan niet exact een parabool is. Draaiing maakt ook de hoek met de bodem na de eerste keer stuiteren scherper dan verwacht. Door inelastische vervorming van de bal bij contact met de grond en door luchtweerstand verliest de bal energie, zodat hij telkens minder hoog komt en op den duur blijft liggen.

Een kogelbaan is de kromme die een voorwerp of projectiel, bijvoorbeeld een kanonskogel, mortiergranaat of golfbal, beschrijft na het afschieten of wegslaan.

Paraboolbaan

In de Nederlandse natuurkundetraditie wordt het woord kogelbaan vaak gebruikt als synoniem met een wiskundige figuur, de parabool. Daar zijn echter wel een paar kanttekeningen bij te maken. Een kogel beschrijft een echte parabool als aan de volgende eisen voldaan is.

1. De horizontale beweging van de kogel moet eenparig zijn, oftewel de horizontale snelheid $v_{x}$ moet constant zijn in de tijd.
2. De verticale beweging moet eenparig versneld of vertraagd zijn, oftewel de verticale snelheid $v_{y}$ moet evenredig met de tijd toe- of afnemen.

Als de luchtweerstand en de kromming van de Aarde verwaarloosd kunnen worden, wordt aan beide eisen voldaan. De kromming van het traject van het projectiel wordt in de ballistiek de kogelval genoemd.

Geschiedenis

De paraboolbaan van kanonskogels werd voor het eerst geopperd door Galilei in de eerste helft van de 17e eeuw. Hij deed dit na proeven of gedachte-experimenten waarbij kogels van een helling rolden. De paraboolbaan voor kogels werd later wiskundig bewezen door Isaac Newton. Voorwerpen die afwijken van een ronde kogelvorm, zoals een duiker die van een duikplank springt, kunnen ingewikkelde bewegingen maken tijdens de sprong, maar het zwaartepunt kan vrijwel niet anders dan een paraboolbaan beschrijven.

Afwijking van de paraboolbaan

Trajecten met luchtweerstand van een projectiel met verschillende mondingssnelheden.

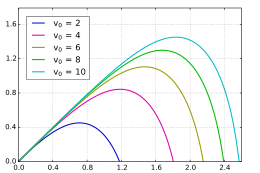
De volgende effecten zijn van invloed op de uitwendige ballistiek van een bal of projectiel:

• Door wind en luchtweerstand wordt de kogelbaan asymmetrisch en wijkt af van een parabool, zoals de animatie en de afbeelding rechts laten zien.
• Een ronddraaiende kogel of bal kan afwijken van de paraboolbaan vanwege het magnuseffect.
• De aardrotatie en het corioliseffect kunnen een afwijking veroorzaken als projectielen over een flinke afstand afgeschoten worden.
• Een eenparige verticale versnelling veronderstelt een uniform gravitatieveld: voor projectielen die zeer grote afstanden afleggen moet soms rekening gehouden worden met de kromming van het aardoppervlak.

De luchtweerstand is voor krombaangeschut doorgaans de belangrijkste oorzaak voor afwijkingen van de paraboolbaan. De luchtweerstand $F_{w}$ wordt voor het grootste deel bepaald door een weerstandscoëfficiënt $C_{w}$ en de snelheid $v$ van het projectiel:

$F_{w}={\tfrac {1}{2}}A\cdot C_{w}\cdot \rho \cdot v^{2}$

waarin $A$ de relatieve oppervlakte van het projectiel is en $\rho$ de luchtdichtheid. Weersomstandigheden als luchtdruk, luchtvochtigheid, regen, windkracht en windrichting kunnen invloed hebben op de kogelbaan. Bij snelheden hoger dan de geluidssnelheid verandert de weerstandscoëfficiënt. Als uitdrukkingen voor de luchtweerstand en het magnuseffect worden toegevoegd aan de bewegingsvergelijkingen voor een projectiel dan krijgt men niet-lineaire dynamische systemen waarvan de vergelijkingen niet eenvoudig oplosbaar zijn. De invloed van verschillende atmosferische omstandigheden op kogelbanen kan alleen door veldonderzoek bepaald worden.

Door balsporters wordt vaak handig gebruik gemaakt van de effecten die afwijkingen van de paraboolbaan veroorzaken.

Voorbeelden:

• In het oppervlak van golfballen zitten putjes, de zogenaamde dimples. De putjes veroorzaken wervelingen die de luchtweerstand en het magnuseffect beïnvloeden.
• Voetballers gebruiken de spin en het magnuseffect om de baan van een voetbal in de gewenste richting te sturen.
• De zware pijlpunten van de pijlen die met een longbow werden afgeschoten stabiliseerden de vlucht van een pijl.
• Het corioliseffect heeft invloed op de baan van projectielen die door groot krombaangeschut, zoals houwitsers en mortieren, worden afgeschoten.
• Geschut met een groot bereik moet rekening houden met de kromming van het aardoppervlak omdat doelen zich meestal achter de horizon bevinden.
• De banen van ballistische raketten die een suborbitale ruimtevlucht maken wijken sterk af van de paraboolbaan maar ze worden amper beïnvloed door atmosferische omstandigheden.

Formules

Voor een horizontaal afgeschoten projectiel waarvoor de luchtweerstand verwaarloosbaar is, wordt het traject gegeven door:

$S_{x}(t)=v\cdot t$

$S_{y}(t)=-{\tfrac {1}{2}}g\cdot t^{2}$

Kogelbaan

Pantserhouwitser

Grote mortier

305mm houwitser

Daarin is:

$S_{x}$ de horizontaal afgelegde afstand (m);

$S_{y}$ de verticaal afgelegde afstand of kogelval (m);

$v$ de mondingssnelheid (m/s), de kogelsnelheid bij het afschieten;

$t$ de tijd (s);

$g$ de valversnelling (m/s²)

Als het projectiel afgeschoten wordt met een elevatie α en een mondingssnelheid $v$ dan wordt dit:

$S_{x}(t)=v\cdot \cos(\alpha )\cdot t$

$S_{y}(t)=v\cdot \sin(\alpha )\cdot t-{\tfrac {1}{2}}g\cdot t^{2}$

Bij het afschieten van een projectiel kent men de positie van het doel $(S_{x},S_{y})$ en de mondingssnelheid $v$ zodat de elevaties direct berekend kunnen worden door middel van:

$\alpha _{1,2}={\tfrac {1}{2}}\arccos \left({\frac {\left({\frac {gS_{x}^{2}}{v^{2}}}\right)S_{y}\pm {\sqrt {S_{x}^{2}S_{y}^{2}+S_{x}^{4}-\left({\frac {gS_{x}^{2}}{v^{2}}}\right)^{2}S_{x}^{2}}}}{S_{x}^{2}+S_{y}^{2}}}\right)$

of

$a_{1,2}=\arctan \left({\frac {v^{2}\pm {\sqrt {v^{4}-g(gS_{x}^{2}+2S_{y}v^{2})}}}{gS_{x}}}\right)$

Er zijn, afhankelijk van de waarde van de discriminant, twee, een of geen oplossingen die een waarde voor de elevatie opleveren.

Schootsbereik

Voor het schootsbereik geldt $\alpha _{1}=\alpha _{2}=\alpha _{max}$, dat wil zeggen als voor de discriminant geldt:

$D=S_{x}^{2}S_{y}^{2}+S_{x}^{4}-\left({\frac {gS_{x}^{2}}{v^{2}}}\right)^{2}S_{x}^{2}=0$

zodat:

$\alpha _{\text{max}}={\tfrac {1}{2}}\arccos \left({\frac {gS_{x}^{2}S_{y}}{v^{2}(S_{x}^{2}+S_{y}^{2})}}\right)$

Hellend terrein

Voor hellend terrein geldt voor de hellingshoek $\beta$:

$\beta =\arcsin(S_{y}/S_{x})$

zodat de discriminant geschreven kan worden als:

$D=\sin ^{2}\beta +1-\left({\frac {g}{v^{2}}}\right)^{2}S_{x}^{2}$

en de elevatie als:

$\alpha _{1,2}={\tfrac {1}{2}}\arccos \left({\frac {({\frac {g}{v^{2}}})S_{x}\sin \beta \pm {\sqrt {D}}}{1+\sin ^{2}\beta }}\right)$

Het schootsbereik wordt gegeven door:

$S_{x}={\frac {v^{2}}{g}}{\sqrt {\sin ^{2}\beta +1}}$

met een elevatie:

$\alpha _{max}={\tfrac {1}{2}}\arccos \left({\frac {\sin \beta }{\sqrt {1+\sin ^{2}\beta }}}\right)$

Vlak terrein

In vlak terrein geldt $S_{y}=0$ zodat:

$\alpha _{1,2}={\tfrac {1}{2}}\arccos \left(\pm {\sqrt {1-\left({\frac {gS_{x}}{v^{2}}}\right)^{2}}}\right)$

Voor het schootsbereik in vlak terrein geldt $\alpha _{max}=45^{\circ }$ en $S_{x}=v^{2}/g$.

Zie ook

• Baan (hemellichaam)
• Eenparig versnelde beweging
• Kogelval
• Paraboolvlucht
• Traject
• Vergelijkingen voor een vallend voorwerp