Mechanische spanning

Een mechanische spanning, in het Engels: stress, is de kracht die wordt uitgeoefend per oppervlakte-eenheid van een voorwerp. Er zijn vijf vormen van spanning: drukspanning, trekspanning, moment, schuifspanning en torsie.
Mechanische spanning vervormt voorwerpen. De mate van vervorming is afhankelijk van de elasticiteit en plasticiteit van het materiaal. Als de spanning de sterkte van het voorwerp overschrijdt, dan bezwijkt het voorwerp.
De vijf vormen van mechanische spanning[bewerken | brontekst bewerken]
Drukspanning[bewerken | brontekst bewerken]
Bij een drukspanning wordt een voorwerp onder druk gezet. Een drukkracht zorgt voor verkorting van het materiaal. Veelal zal het materiaal ook dikker worden. Een langwerpig voorwerp, bijvoorbeeld een kolom in een bouwwerk, bezwijkt al bij een lagere druk dan de druk waaronder het materiaal bezwijkt. Een langwerpig voorwerp kan namelijk knikken. Een boogbrug is een succesvol brugtype, omdat het gewicht van de brug heel gelijkmatig opgevangen kan worden met drukspanning in de boog. Er zijn wel maatregelen nodig om een knik in de boog te voorkomen.
Trekspanning[bewerken | brontekst bewerken]

Trekspanning of rekspanning is tegengesteld aan drukspanning. Het materiaal waarop een trekkracht werkt, wil uitrekken. Een voorwerp waaraan wordt getrokken, wordt niet alleen langer, maar ook dunner. Dit verschijnsel wordt dwarscontractie genoemd. Een hangbrug is een succesvol brugtype voor bruggen, omdat het gewicht opgevangen kan worden met trekspanning. Omdat bij trekspanning geen rekening gehouden hoeft te worden met knik kan het materiaal tot zijn maximum sterkte (met inachtneming van een veiligheidsfactor) belast worden.
Buiging of moment[bewerken | brontekst bewerken]
Buiging ontstaat als een balk, profiel of een plaat in de dwarsrichting belast wordt. Denk aan een balk over een sloot, waarop in het midden een persoon staat. De persoon in het midden oefent een neerwaartse kracht op de balk uit, en de beide oevers oefenen een opwaartse kracht op de balk uit. De balk heeft daardoor de neiging te buigen. De kracht die deze buiging veroorzaakt is het moment. Een moment kan ontbonden worden in druk- en trekkrachten. In de balk in dit voorbeeld staat de bovenzijde van de balk bloot aan drukspanning, en de onderzijde aan trekspanning. Het deel van de balk dat zich precies midden tussen de bovenzijde en de onderzijde van de balk bevindt is er geen druk- of trekspanning. De trek- en drukspanning aan de boven- respectievelijk onderzijde van de balk zijn niet overal even groot. De spanning is het grootst op het punt waar de balk belast wordt, en loopt af tot nul aan de uiteinden van de balk. Het gewicht van de balk zelf belast de balk ook, en veroorzaakt dus ook moment. Als de persoon op de balk te zwaar is voor de balk, zal de balk bezwijken op de plaats waar het moment het grootste is. Zolang het gewicht van de balk een bijrol speelt, zal dat zijn op de plaats waar de persoon staat.
Schuifspanning[bewerken | brontekst bewerken]
Schuifspanning ontstaat als een profiel of een plaat in de dwarsrichting wordt belast. Denk aan een stapel boeken die je met één hand tilt, met je andere hand erbovenop. Als je de boeken sterk genoeg op elkaar klemt kun je de hele stapel een kwartslag draaien van de verticale stand naar een horizontale stand, zonder dat de boeken vallen. Door de druk is de schuifweerstand tussen de boeken zo groot dat de stapel niet bezwijkt onder schuifkrachten. Als je moe wordt en niet meer hard genoeg drukt 'bezwijkt' de stapel boeken.
Wring of torsie[bewerken | brontekst bewerken]
Torsie of wring ontstaat als een profiel om zijn lengteas gedraaid wordt. Denk aan aandrijfas van een voertuig, of aan een boring naar olie of gas. De boorkop bevindt zich honderden meters of kilometers onder de grond en hij wordt aangedreven via een lange pijp. Deze pijp ondervindt torsie. Torsie vervormt de pijp, zodat de boorkop ettelijke omwentelingen achter kan lopen op zijn aandrijfmechanisme. Torsie kan ontbonden worden in schuifkrachten, waarbij de schuifkracht toeneemt naarmate het verder is verwijderd van het zwaartepunt van het profiel. Bij een gelijke hoeveelheid materiaal per meter (ofwel een gelijk gewicht per meter) is een holle staaf daarom veel beter in staat om torsie op te nemen dan een massieve staaf.
Mechanische spanning[bewerken | brontekst bewerken]

De mechanische spanningen op een oppervlak zijn onder te verdelen in spanningen die loodrecht op het oppervlak werken, de normaalspanningen , en spanningen die parallel aan het oppervlak lopen, de schuifspanningen .
Normaalspanning[bewerken | brontekst bewerken]
Als druk- of trekspanning loodrecht op het oppervlak van een voorwerp wordt uitgeoefend, dan is de spanning te berekenen als de kracht gedeeld door de oppervlakte waarop hij wordt uitgeoefend. Spanning wordt uitgedrukt met de Griekse letter sigma. Onderscheid kan worden gemaakt tussen één-assige krachten en mechanische spanningen ,
waarbij:
- de toegepaste normaalspanning (Pa) is;
- de toegepaste kracht (N) is en
- de oppervlakte is waarop de kracht aangrijpt (m²).
De SI-eenheid voor kracht is newton, afgekort als N. is het oppervlak van de doorsnede waar de kracht op werkt met als eenheid m². De SI-eenheid voor druk is dus N/m² ofwel pascal, afgekort Pa. In berekeningen van constructies wordt vaak N/mm² gebruikt. 1 N/mm² is gelijk aan 1.000.000 Pa of 1 MPa.

Schuifspanning[bewerken | brontekst bewerken]
Een eenvoudige definitie van een schuifspanning is, 'De componenten van een spanning op een punt die parallel staan aan het vlak waarin zij liggen'. De schuifspanning wordt gegeven door:
waarbij:
- de schuifspanning in Pa, MPa of N/mm2 is,
- de toegepaste kracht in N en
- het oppervlak waarover de kracht werkt in m2.
Directe afschuiving van een object door het uitoefenen van een moment, zal behalve een schuifkracht ook een trekspanning en drukspanning geven.
Meer-assige spanningen[bewerken | brontekst bewerken]

Dimensies[bewerken | brontekst bewerken]
De spanningsvectoren kunnen worden georiënteerd op een denkbeeldig assenstelsel. Op die manier kan er onderscheidt worden gemaakt tussen één-assige spanningstoestanden en meer-assige spanningstoestanden. In de meeste situaties kan er gesproken worden over een van de volgende drie toestanden:
- 1D – één-assige spanningstoestand
- 2D – twee-assige spanningstoestand
- 3D – drie-assige spanningstoestand
Lasten[bewerken | brontekst bewerken]
De krachten kunnen op verschillende manieren op een oppervlak inwerken. Deze soorten lasten zijn: puntlasten, lijnlasten en vlaklasten:
- Puntlast: een puntlast is een kracht of moment die op een welbepaald punt inwerkt op de constructie. In de praktijk worden daar alle lasten toe gerekend waarvan de oppervlakte waarop de last inwerkt klein is in verhouding tot de oppervlakte van het constructieonderdeel. Enkele voorbeelden: een kolom op een vloer, een balk op een muur, een geparkeerde auto in een parkeergarage.
- Lijnlast: een lijnlast is een kracht of moment die inwerkt over een zekere lengte van een constructieonderdeel. De grootte van de belasting kan gelijkmatig zijn verdeeld of variëren over de lengte waarop de lijnlast inwerkt. Een voorbeeld van een lijnlast is een wand op een vloer.
- Vlaklast: een vlaklast is een kracht die inwerkt over een zeker oppervlak. Deze last kan gelijkmatig verdeeld zijn, zoals sneeuwbelasting op een dak, of variëren over de lengte en/of breedte van de constructie, zoals de waterdruk op een stuwdam of de gronddruk tegen een keermuur.
Tensorgrootheid[bewerken | brontekst bewerken]
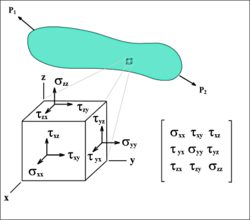
Mechanische spanning werkt op een oppervlak. Als de spanning loodrecht op het oppervlak van een voorwerp werkt, spreekt men van normaalspanning. Dit is in de natuur meestal niet het geval, de spanning staat meestal onder een (niet loodrechte) hoek met het oppervlak van het voorwerp waar de spanning op werkt. De spanning kan in dat geval verdeeld worden over drie componenten, in elke ruimtelijke dimensie een. De component loodrecht op het oppervlak is de normaalspanning, de componenten parallel aan het oppervlak zijn de schuifspanningscomponenten (aangegeven met ).
In de continuümmechanica is de spanningstoestand op een bepaald punt in een continuüm te benaderen door dit punt als een infinitesimaal klein kubusje te zien. Op alle zijden van het kubusje staat een bepaalde spanning, te verdelen in drie componenten. Als we aannemen dat de kubus in evenwicht verkeert, is de spanning op parallelle zijden gelijk, zodat drie zijden overblijven met elk drie componenten. Deze in totaal negen componenten kunnen in een drie bij drie tensor worden gezet:
Dit is een symmetrische matrix, de spanningstensor is dus een voorbeeld van een symmetrische tensor.
Conventies voor grootheid[bewerken | brontekst bewerken]
De grootheid wordt vaak als σ aangeduid, maar ook komt voor. Voor de tensor geldt hetzelfde. Voor de notatie van de componenten van de tensor maakt men vaak geen onderscheid tussen diagonaalelementen en niet-diagonaalelementen; voor beide gebruikt men dan ofwel σ ofwel .












