Trapezoëder

Trapezoëder
Vlakken	2n vliegers
Zijden	2n
Hoekpunten	2n+2
Ribben	4n
Zijvlakken per hoekpunt	3
Ribben per zijvlak	4 of 6
Schläfli-symbool	{ } ⨁ {n}
Symmetriegroep	Dnd
Eigenschappen	convex isohedraal
Duaal veelvlak	antiprisma
Portaal    Wiskunde

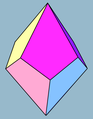
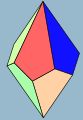
Een trapezoëder of antidipiramide is een veelvlak met 2$n$ zijvlakken, die het duale veelvlak van een antiprisma is. De veelvlakken, die aan deze definitie voldoen en die spiegelsymmetrisch zijn, hebben vliegers als zijvlakken. Een ruitenzesvlak is hier een voorbeeld van, omdat een ruit als vlieger telt. Een spiegelsymmetrische trapezoëder met zes zijvlakken is een ruitenzesvlak.

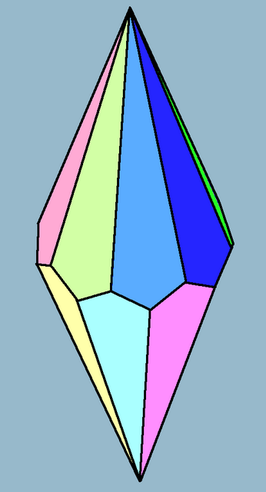
Varianten

Hieronder staan voorbeelden van trapezoëders. Bij de trapezoëders waarvan de zijvlakken vliegers zijn, staat per figuur het aantal zijvlakken.

• 
  6
• 
  8
• 
  10
• 
  trapezoëder, maar niet spiegelsymmetrisch
• 
  antiprisma tussen twee regelmatige zeshoeken

Bronnen, noten en/of referenties